
题目列表(包括答案和解析)
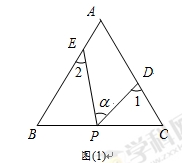
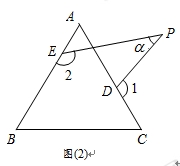

问题背景:已知x是实数,求![]() 的最小值。要解决这个问题需现判断出0<x<12,继而联想到构造以边长为2+3和12为边的矩形,找出等于
的最小值。要解决这个问题需现判断出0<x<12,继而联想到构造以边长为2+3和12为边的矩形,找出等于![]() 的线段,再比较
的线段,再比较![]() 和矩形对角线的大小。
和矩形对角线的大小。
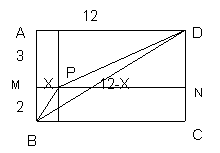 解:构造矩形ABCD,使AB=5,AD=12.在AB上截取AM=3,做矩形AMND。设点P是MN上一点MP=x,则PN=12-x,
解:构造矩形ABCD,使AB=5,AD=12.在AB上截取AM=3,做矩形AMND。设点P是MN上一点MP=x,则PN=12-x,

(1) 我们把上述求最值问题的方法叫做构图法.请仿造上述方法求![]() 的最小值。
的最小值。
探索创新:
(2)已知a,b,c,d是正实数且a+b+c+d=1,试运用构图法求![]() 的最小值.
的最小值.
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=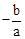 ,x1•x2=
,x1•x2=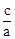 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|=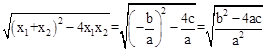
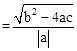 。
。
参考以上定理和结论,解答下列问题:
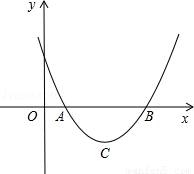
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.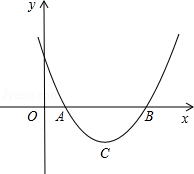
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=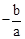 ,x1•x2=
,x1•x2=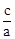 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|=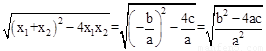
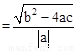 。
。
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com