
题目列表(包括答案和解析)
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:


(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围.
若因为时间不够等方面的原因,经过探索、思考仍无法圆满解答本题,请不要轻易放弃,试试将上述(2)、(3)小题换为下列问题解答(已知条件及第(1)小题与上相同,完全正确解答只能得到5分):
(2)若点D的坐标为(1,0),求矩形DEFG的面积.
(本小题满分10分)
数形结合作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,即“以数解形”;或者借助形的几何直观性来阐明数之间的某种关系,即 “以形助数”。
 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
(1)请你用数形结合的“以数解形”思想来解:如图2,已知在△ABC中(AC>BC),∠ACB=900,CD⊥AB,D为垂足, CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根,求AD、MD的长。
(2)请你用数形结合的“以形助数”思想来解: 设a、b、c、d都是正数,满足a:b=c:d,且a最大。求证:a+d>b+c(提示:不访设AB=a,CD=d,AC=b,BC=c,构造图1)
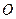 和
和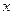 轴上另一点
轴上另一点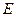 ,顶点
,顶点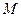 的坐标为
的坐标为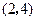 ;矩形
;矩形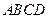 的顶点
的顶点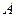 与点
与点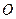 重合,
重合,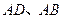 分别在
分别在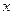 轴、
轴、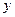 轴上,且
轴上,且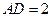 ,
,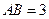 .
.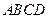 以每秒1个单位长度的速度从图1所示的位置沿
以每秒1个单位长度的速度从图1所示的位置沿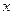 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点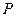 也以相同的速度从点
也以相同的速度从点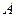 出发向
出发向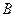 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为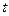 秒(
秒(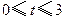 ),直线
),直线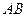 与该抛物线的交点为
与该抛物线的交点为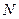 (如图2所示).
(如图2所示).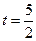 时,判断点
时,判断点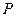 是否在直线
是否在直线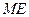 上,并说明理由;
上,并说明理由;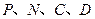 为顶点的多边形面积为
为顶点的多边形面积为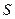 ,试问
,试问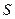 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.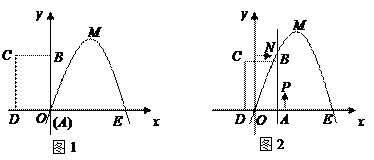
(本小题满分12分)如图1,已知抛物线经过坐标原点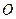 和
和 轴上另一点
轴上另一点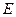 ,顶点
,顶点 的坐标为
的坐标为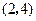 ;矩形
;矩形 的顶点
的顶点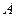 与点
与点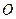 重合,
重合,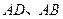 分别在
分别在 轴、
轴、 轴上,且
轴上,且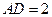 ,
, .
.
(1)求该抛物线所对应的函数关系式;
(2)将矩形 以每秒1个单位长度的速度从图1所示的位置沿
以每秒1个单位长度的速度从图1所示的位置沿 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点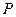 也以相同的速度从点
也以相同的速度从点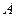 出发向
出发向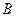 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为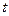 秒(
秒(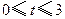 ),直线
),直线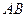 与该抛物线的交点为
与该抛物线的交点为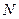 (如图2所示).
(如图2所示).
①当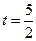 时,判断点
时,判断点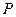 是否在直线
是否在直线 上,并说明理由;
上,并说明理由;
②设以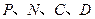 为顶点的多边形面积为
为顶点的多边形面积为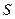 ,试问
,试问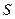 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.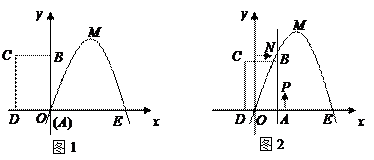
(本小题满分10分)
数形结合作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,即 “以数解形”;或者借助形的几何直观性来阐明数之间的某种关系,即 “以形助数”。
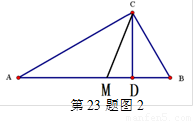 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
(1)请你用数形结合的“以数解形”思想来解:如图2,已知在△ABC中(AC>BC),∠ACB=900,CD⊥AB,D为垂足, CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根,求AD、MD的长。
(2)请你用数形结合的“以形助数”思想来解: 设a、b、c、d都是正数,满足a:b=c:d,且a最大。求证:a+d>b+c(提示:不访设AB=a,CD=d,AC=b,BC=c,构造图1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com