
题目列表(包括答案和解析)
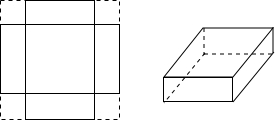
现有一张长19 cm,宽15 cm的长方形纸片,四角剪去一个小正方形,做成底面积为![]() 的无盖长方体纸盒,若设剪去的小正方形的边长为
的无盖长方体纸盒,若设剪去的小正方形的边长为![]() cm,则可列出方程( ).
cm,则可列出方程( ).
A
.(19+2C
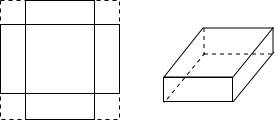
.(19+2现有一张长19 cm,宽15 cm的长方形纸片,四角剪去一个小正方形,做成底面积为![]() 的无盖长方体纸盒,若设剪去的小正方形的边长为
的无盖长方体纸盒,若设剪去的小正方形的边长为![]() cm,则可列出方程( ).
cm,则可列出方程( ).
A
.(19+2C
.(19+2| a2+b2 |
| b2+c2 |
| c2+a2 |
| 2 |
 +b+c的正方形来研究.
+b+c的正方形来研究.| a2+b2 |
| b2+c 2 |
| a2+c2 |
| a2+b2 |
| b2+c2 |
| c2+a2 |
| 2 |
| x2+4 |
| y2+9 |
| a2+b2 |
| 4a2+b2 |
| a2+4b2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com