甲、乙两同学对关于y、x的抛物线f：y＝x²－2mx＋2m²＋2m进行探讨交流时，各得出一个结论．

甲同学：当抛物线f经过原点时，顶点在第三象限平分线所在的直线上；

乙同学：不论m取什么实数值，抛物线f顶点一定不在第四象限．

（1）请你求出抛物线f经过原点时m的值及顶点坐标，并说明甲同学的结论是否正确？

（2）乙同学的结论正确吗？若你认为正确，请求出当实数m变化时，抛物线f顶点的纵横坐标与m之间的函数关系式，并说明顶点不在第四象限的理由；若你认为不正确，求出抛物线f顶点在第四象限时，m的取值范围．

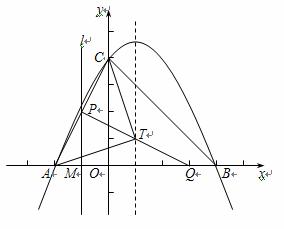
如图，抛物线：y＝ax²＋bx＋4与x轴交于点A(－2，0)和B(4，0)、与y轴交于点C．
(1)求抛物线的解析式；
(2)T是抛物线对称轴上的一点，且△ACT是以AC为底的等腰三角形，求点T的坐标；
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行．当点M原点时，点Q立刻掉头并以每秒个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动．过点M的直线l⊥轴，交AC或BC于点P．求点M的运动时间t(秒)与△APQ的面积S的函数关系式，并求出S的最大值．

如图，抛物线：y＝ax²＋bx＋4与x轴交于点A(－2，0)和B(4，0)、与y轴交于点C．

(1)求抛物线的解析式；

(2)T是抛物线对称轴上的一点，且△ACT是以AC为底的等腰三角形，求点T的坐标；

(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行．当点M原点时，点Q立刻掉头并以每秒个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动．过点M的直线l⊥轴，交AC或BC于点P．求点M的运动时间t(秒)与△APQ的面积S的函数关系式，并求出S的最大值．