
题目列表(包括答案和解析)
已知:如图,四边形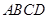 是平行四边形,
是平行四边形,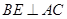 于
于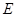 ,
,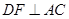 于
于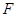 .求证:
.求证: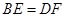 .
.
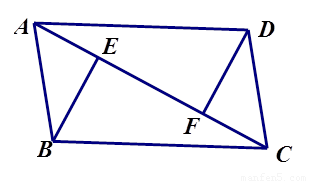
【解析】证线段所在的三角形全等.根据“AAS”可证△ABE≌△CDF或△ADF≌△CBE.
如图,已知以△ABC的边AC、BC分别向外作正方形ACDE和正方形BCFG.
求证:BD=AF.

欲证BD=AF,可证△ACF≌△DCB,由正方形ACDE和正方形BCFG可知AC=DC,CF=CB,∠ACD=∠BCF=90°,易证结论成立.
证明:∵四边形ACDE和四边形BCFG是正方形
∴AC=DC,CF=CB,∠ACD=∠BCF=90°
(正方形四个角都是________,四条边都________)
∴∠ACD+∠ACB=∠BCF+∠ACB
即∠ACF+∠DCB
∴△ACF≌△________(SAS)
∴AF=BD

 辨析纠错
辨析纠错湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com