
题目列表(包括答案和解析)
 如图1.已知Rt△ABC,∠C=90°,∠A=30°,AB=2,M是斜边AB上的一个动点,垂足为H,以MH为对角线作菱形MPHQ,其中,顶点P始终在斜边AB上.连接PQ并延长交AC于点E,以E为圆心,EC长为半径作⊙E.
如图1.已知Rt△ABC,∠C=90°,∠A=30°,AB=2,M是斜边AB上的一个动点,垂足为H,以MH为对角线作菱形MPHQ,其中,顶点P始终在斜边AB上.连接PQ并延长交AC于点E,以E为圆心,EC长为半径作⊙E.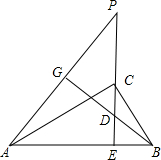 如图,已知CE是Rt△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,BG⊥AP垂足为G,交CE于D,
如图,已知CE是Rt△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,BG⊥AP垂足为G,交CE于D,

如图1,已知,CE是Rt△ABC的斜边AB上的高,点P是CE的延长线上任意一点,BG⊥AP,
求证:(1)△AEP∽△DEB
(2) CE2=ED·EP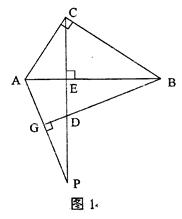
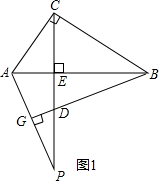
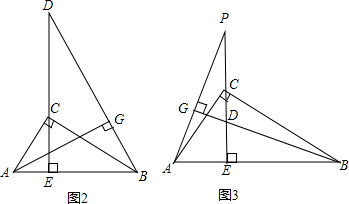
若点P在线段CE上或EC的延长线上时(如图2和图3),上述结论CE2=ED·EP还成立吗?若成立,请给出证明;若不成立,请说明理由.(图2和图3挑选一张给予说明即可)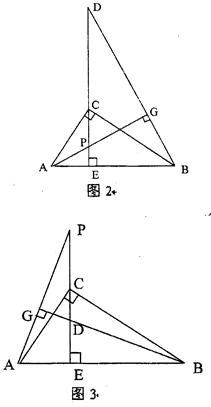
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com