
题目列表(包括答案和解析)
 如图,等边△ADE是由△ABC绕点A逆时针旋转40°得到的,其中AC与DE相交于点F,则∠AFD=
如图,等边△ADE是由△ABC绕点A逆时针旋转40°得到的,其中AC与DE相交于点F,则∠AFD= 如图,等边△ADE是由△ABC绕点A逆时针旋转40°得到的,其中AC与DE相交于点F,则∠AFD=________度.
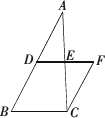
如图,等边△ADE是由△ABC绕点A逆时针旋转40°得到的,其中AC与DE相交于点F,则∠AFD=________度.如图,在△ABC中,AB=2BC,点D、E分别为AB、AC的中点,连结DE,将△ADE绕点E旋转180°后得到△CFE.试判断四边形BCFD的形状,并说明理由.(提示:一组对边平行且相等的四边形是平行四边形;连结三角形两边中点的线段平行于第三边,且等于第三边长的一半.)

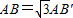 ,
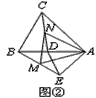
,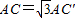 ,连接B′C′,将△AB′C′绕点A逆时针旋转角θ (0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图3探索∠BOE的度数,直接写出结果,不必说明理由.
,连接B′C′,将△AB′C′绕点A逆时针旋转角θ (0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图3探索∠BOE的度数,直接写出结果,不必说明理由.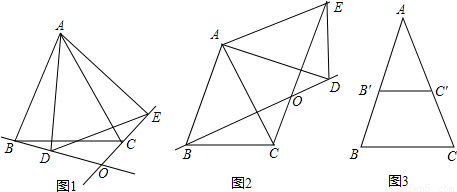
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com