已知△ABC，分别以AB、AC为边作△ABD和△ACE，且AD=AB，AC=AE，∠DAB=∠CAE，连接DC与BE，G、F分别是DC与BE的中点．
（1）如图1，若∠DAB=60°，则∠AFG=______；如图2，若∠DAB=90°，则∠AFG=______；
（2）如图3，若∠DAB=α，试探究∠AFG与α的数量关系，并给予证明；
（3）如果∠ACB为锐角，AB≠AC，∠BAC≠90°，点M在线段BC上运动，连接AM，以AM为一边以点A为直角顶点，且在AM的右侧作等腰直角△AMN，连接NC；试探究：若NC⊥BC（点C、M重合除外），则∠ACB等于多少度？画出相应图形，并说明理由．（画图不写作法）

探究问题

(1)阅读理解：

①如图1，在△ABC所在平面上存在一点P，使它到三角形三顶点的距离之和最小，则称点P为△ABC的费马点，此时PA＋PB＋PC的值为△ABC的费马距离．

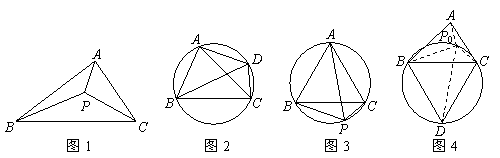②如图2，若四边形ABCD的四个顶点在同一个圆上，则有AB·CD＋BC·AD＝AC·BD．此为托勒密定理．

(2)知识迁移：

①请你利用托勒密定理，解决如下问题：

如图3，已知点P为等边△ABC外接圆的弧BC_{上任意一点．求证：PB＋PC＝PA．}

②根据(2)①的结论，我们有如下探寻△ABC(其中∠A、∠B、∠C均小于120º)的费马点和费马距离的方法：

第一步：如图4，在△ABC的外部以BC为边长作等边△BCD及其外接圆；

第二步：在弧BC上取一点P₀，连接P₀A、P₀B、P₀C、P₀D．

易知P₀A＋P₀B＋P₀C＝P₀A＋(P₀B＋P₀C)＝P₀A＋　　　 ；

第三步：请你根据(1)①中定义，在图4中找出△ABC的费马点P，线段　 　的长度即为△ABC的费马距离．

(3)知识应用：

2010年4月，我国西南地区出现了罕见的持续干旱现象，许多村庄出现了人、畜饮水困难．为解决老百姓饮水问题，解放军某部到云南某地打井取水．

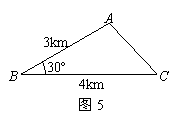已知三村庄A、B、C构成了如图5所示的△ABC(其中∠A、∠B、∠C均小于120º)，现选取一点P打水井，使水井P到三村庄A、B、C所铺设的输水管总长度最小．求输水管总长度的最小值．

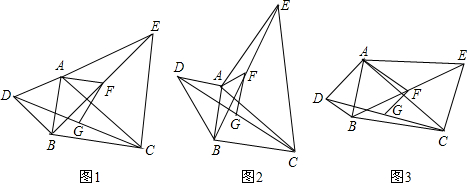
已知△ABC，分别以AB、AC为边作△ABD和△ACE，且AD=AB，AC=AE，∠DAB=∠CAE，连接DC与BE，G、F分别是DC与BE的中点．

（1）如图1，若∠DAB =60°，则∠AFG=__     ____；

如图2，若∠DAB =90°，则∠AFG=____     __；

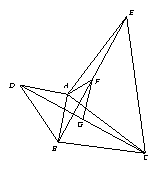
图1                                    图2

（2）如图3，若∠DAB =，试探究∠AFG与的数量关系，并给予证明．；

（3）如果∠ACB为锐角，AB≠AC，∠BAC≠90º，点M在线段BC上运动，连接AM，以AM为一边以点A为直角顶点，且在AM的右侧作等腰直角△AMN，连接NC；

试探究：若NC⊥BC（点C、M重合除外），则∠ACB等于多少度？画出相应图形，并说明理由．（画图不写作法）