
题目列表(包括答案和解析)
 MD;
MD;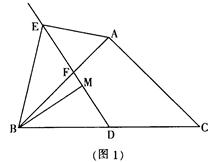

 ,求tan∠ACP的值.
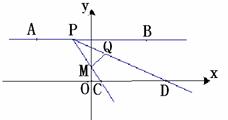
,求tan∠ACP的值.已知如图,在平面直角坐标系中有四点,坐标分别为A(-4,3)、B(4,3)、
M(0,1)、Q(1,2),动点P在线段AB上,从点A出发向点B以每秒1个单位运动。连结PM、PQ并延长分别交X轴于C、D两点(如图).
(1)在点P移动的过程中,若点M、C、D、Q能围成四边形,则t的取值范围是__________,并写出当t=2时,点C的坐标________.
(2)在点P移动的过程中,△PMQ可能是轴对称图形吗?若能,请求出符合条件的点P的坐标;若不能,请说明理由.
(3)在点P移动的过程中,求四边形MCDQ的面积S的范围.


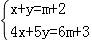 的解是一对正数.
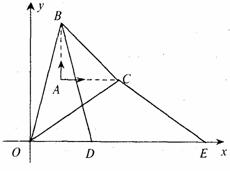
的解是一对正数.如图,已知点A的坐标为(2,4),在点A处有二只蚂蚁(忽略其大小),它们
同时出发,一只以每秒1个单位的速度垂直向上爬行,另一只同样以每秒1个单位的速度水平
向右爬行,t秒后,它们分别到达B、C处,连接BC.若在x轴上有两点D、E,
满足DB=OB,EC=OC,则
(1)当t=l秒时,求BC的长度;
(2)证明:无论t为何值,DE=2AC始终成立;
(3)延长BC交x轴于点F,当t的取值范围是 ,点F始终![]() 在点E的左侧。(请直接写出结果,无需书写解答过程!)
在点E的左侧。(请直接写出结果,无需书写解答过程!)
阅读理解:对于任意正实数a、b,∵ ≥0,∴
≥0,∴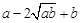 ≥0,
≥0,
∴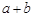 ≥
≥ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在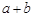 ≥
≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 .
.
(1)根据上述内容,回答下列问题:现要制作一个长方形(或正方形),使镜框四周围成的面积为4,请设计出一种方案,使镜框的周长最小。
设镜框的一边长为m(m>0),另一边的为 ,考虑何时时周长
,考虑何时时周长 最小。
最小。
∵m>0,  (定值),由以上结论可得:
(定值),由以上结论可得:
只有当m= 时,镜框周长 有最小值是 ;
有最小值是 ;
(2)探索应用:如图,已知A(-3,0),B(0,-4),P为双曲线 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com