
题目列表(包括答案和解析)
如图,△ABC为锐角三角形,向形外作正方形ACDE和正方形ABGF,连接FE,求证:S△AFE=S△ABC
证明:过点C作CM⊥AB于M,过点E作EN⊥FA交FA的延长线于N,
∴∠AMC=∠ANE=90°
∵ACDE是正方形 ∴AE=AC ∠EAC=90° ∴∠2+∠3=90°
又∵ABGF是正方形 ∴∠FAB=90° ∴∠BAN=90°
∴∠1+∠2=90° ∴∠1=∠3 ∴Rt△AMC≌Rt△ANE
∴CM=EN 又∵ABGF是正方形 ∴AF=AB
S△AFE=![]() AF?EN S△ABC=
AF?EN S△ABC=![]() AB?CM
AB?CM
∴S△AFE=S△ABC
请你再用另一种方法证明S△AFE=S△ABC.
(过点B作AC的垂线,过F点作AE的垂线与上面证法属同一种方法)


 8、如图,D是△ABC的AB边上的一点,过,点D作DE∥BC交AC于E,若DE:BC=2:5,则AE:EC等于( )
8、如图,D是△ABC的AB边上的一点,过,点D作DE∥BC交AC于E,若DE:BC=2:5,则AE:EC等于( )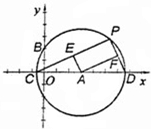 8、如图,以A(3,0)为圆心作⊙A,⊙A与y轴相交B(0,2),与x轴交于点C、D,P为⊙A上不同于C、D的任意一点,连接PC、PD,过A分别作AE⊥PC,AF⊥PD,设点P的横坐标为x,AE2+AF2=y,当点P在⊙A上顺时针从C运动到D的过程中,下列图象能表示y与x函数关系的图象是( )
8、如图,以A(3,0)为圆心作⊙A,⊙A与y轴相交B(0,2),与x轴交于点C、D,P为⊙A上不同于C、D的任意一点,连接PC、PD,过A分别作AE⊥PC,AF⊥PD,设点P的横坐标为x,AE2+AF2=y,当点P在⊙A上顺时针从C运动到D的过程中,下列图象能表示y与x函数关系的图象是( ) 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交与点O,AD与BC交与点P,BE与CD交与点Q,连接PQ.有下列结论:①AD=BE;②AP=BQ;③∠AOB=60°;④DE=DP,其中正确的结论有( )
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交与点O,AD与BC交与点P,BE与CD交与点Q,连接PQ.有下列结论:①AD=BE;②AP=BQ;③∠AOB=60°;④DE=DP,其中正确的结论有( ) 如图,在正方形ABCD中,AB=1,E,F分别是边BC,CD上的点,连接EF、AE、AF,过A作AH⊥EF于点H.若EF=BE+DF,那么下列结论:①AE平分∠BEF;②FH=FD;③∠EAF=45°;④S△EAF=S△ABE+S△ADF;⑤△CEF的周长为2.其中正确结论的个数是( )
如图,在正方形ABCD中,AB=1,E,F分别是边BC,CD上的点,连接EF、AE、AF,过A作AH⊥EF于点H.若EF=BE+DF,那么下列结论:①AE平分∠BEF;②FH=FD;③∠EAF=45°;④S△EAF=S△ABE+S△ADF;⑤△CEF的周长为2.其中正确结论的个数是( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com