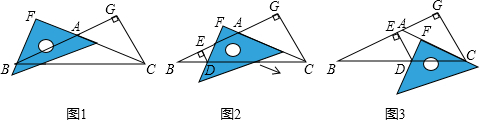
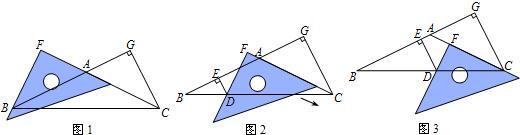
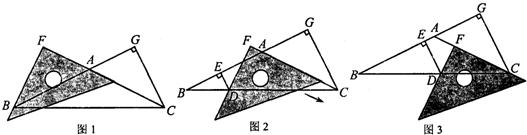
28、在△ABC中,AB=AC,∠ACB=∠ABC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.
(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;
(2)当三角尺沿AC方向平移到图2所在的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE、DF与CG之间满足的数量关系,然后证明你的猜想;(提示:过点D作DH⊥CG,可得四边形EDHG是长方形)
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,试猜想DE,DF与CG之间满足的数量关系.(不用说明理由)



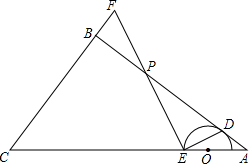 心作半圆,与边AB相切于点D,交线段OC于点E,作EP⊥ED,交射线AB于点P,交射线CB于点F.
心作半圆,与边AB相切于点D,交线段OC于点E,作EP⊥ED,交射线AB于点P,交射线CB于点F.