
题目列表(包括答案和解析)
| 1 | 2 |
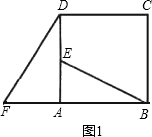
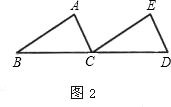
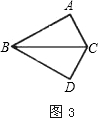
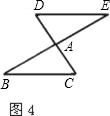



如图,是三张方格纸,请你利用它们解决下列问题:
在图一中画出直线AB的平行线CD;
在图二中画出直线m的垂线n;
在图三中画一个斜放的正方形EFGH
如图3,甲转盘被分成3个面积相等的扇形,乙转盘被分成2个面积相等的扇形.随机地转动指针(当指针指在边界线上时视为无效,重转).
请解答下列问题.
⑴ 在图甲中,随机地转动指针,指针指向扇形2的概率是_____________;
⑵ 分别转动图甲和图乙的指针,两个指针停止时所指区域内的数之和为6或7,试用树状图或列表法求出其概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com