
题目列表(包括答案和解析)
| MM′ | N′N |
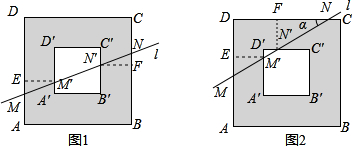
(9分)我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,易知方形环四周的宽度相等.

一条直线l与方形环的边线有四个交点![]() 、
、![]() 、
、![]() 、
、![]() .小明在探究线段
.小明在探究线段![]() 与
与![]() 的数量关系时,从点
的数量关系时,从点![]() 、
、![]() 向对边作垂线段
向对边作垂线段![]() 、
、![]() ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
⑴当直线l与方形环的对边相交时(如图1),直线l分别交![]() 、
、![]() 、
、![]() 、
、![]() 于
于![]() 、
、![]() 、
、![]() 、
、![]() ,小明发现
,小明发现![]() 与
与![]() 相等,请你帮他说明理由;
相等,请你帮他说明理由;
⑵当直线l与方形环的邻边相交时(如图2),l分别交![]() 、
、![]() 、
、![]() 、
、![]() 于
于![]() 、
、![]() 、
、![]() 、
、![]() ,l与
,l与![]() 的夹角为
的夹角为![]() ,你认为
,你认为![]() 与
与![]() 还相等吗?若 相等,说明理由;若不相等,求出
还相等吗?若 相等,说明理由;若不相等,求出![]() 的值(用含
的值(用含![]() 的三角函数表示).
的三角函数表示).

 、
、 、
、 、
、 .小明在探究线段
.小明在探究线段 与
与 的数量关系时,从点
的数量关系时,从点 、
、 向对边作垂线段
向对边作垂线段 、
、 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: 、
、 、
、 、
、 于
于 、
、 、
、 、
、 ,小明发现
,小明发现 与
与 相等,请你帮他说明理由;
相等,请你帮他说明理由; 、
、 、
、 、
、 于
于 、
、 、
、 、
、 ,l与
,l与 的夹角为
的夹角为 ,你认为
,你认为 与
与 还相等吗?若 相等,说明理由;若不相等,求出
还相等吗?若 相等,说明理由;若不相等,求出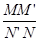 的值(用含
的值(用含 的三角函数表示).
的三角函数表示).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com