
题目列表(包括答案和解析)
| 1 | 3 |

 =
= S△ABC,请证明;
S△ABC,请证明; 与S四边形ABCD之间的数量关系;
与S四边形ABCD之间的数量关系; ;
;某课题研究小组就图形面积问题进行专题研究,他们发现如下结论:
(1)有一![]() 条边对应相等的两个三角形面积之比等于这条边上的对应高之比;
条边对应相等的两个三角形面积之比等于这条边上的对应高之比;
(2)有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比;
…
现请你继续对下面问题进行探究,探究过程可直接应用上述结论.(S表示面积)
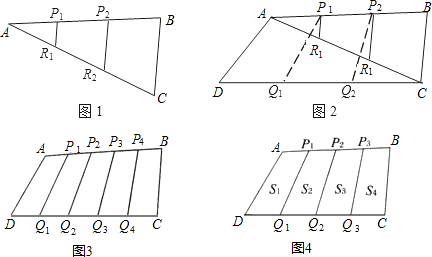
问题1:如图1,现有一块三角形纸板ABC,P1,P2三等分边AB,R1,R2三等分边AC.

 经探究知
经探究知![]() =
=![]() S△ABC,请证明.
S△ABC,请证明.
问题2:若有另一块三角形纸板,可将其与问题1中的拼合成四边形ABCD,如图2,Q1,Q2三等分边DC.请探究![]() 与S四边形ABCD之间的数量关系.
与S四边形ABCD之间的数量关系.
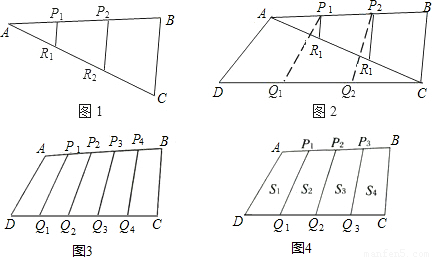
问题3:如图3,P1,P2,P3,P4五等分边AB,Q1,Q2,Q3,Q4五等分边DC.若
S四边形ABCD=1,求![]() .
.
问题4:如图4,P1,P2,P3四等分边AB,Q1,Q2,Q3四等分边DC,P1Q1,P2Q2,P3Q3
 将四边形ABCD分成四个部分,面积分别为S1,S2,S3,S4.请直接写出含有S1,S2,S3,S4的一个等式.
将四边形ABCD分成四个部分,面积分别为S1,S2,S3,S4.请直接写出含有S1,S2,S3,S4的一个等式.

某课题研究小组就图形面积问题进行专题研究,他们发现如下结论:
(1)有一![]() 条边对应相等的两个三角形面积之比等于这条边上的对应高之比;
条边对应相等的两个三角形面积之比等于这条边上的对应高之比;
(2)有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比;
…
现请你继续对下面问题进行探究,探究过程可直接应用上述结论.(S表示面积)
问题1:如图1,现有一块三角形纸板ABC,P1,P2三等分边AB,R1,R2三等分边AC.

经探究知![]() =
=![]() S△ABC,请证明.
S△ABC,请证明.
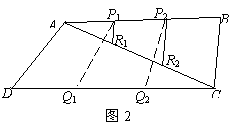
问题2:若有另一块三角形纸板,可将其与问题1中的拼合成四边形ABCD,如图2,Q1,Q2三等分边DC.请探究![]() 与S四边形ABCD之间的数量关系.
与S四边形ABCD之间的数量关系.
问题3:如图3,P1,P2,P3,P4五等分边AB,Q1,Q2,Q3,Q4五等分边DC.若
S四边形ABCD=1,求![]() .
.
问题4:如图4,P1,P2,P3四等分边AB,Q1,Q2,Q3四等分边DC,P1Q1,P2Q2,P3Q3
将四边形ABCD分成四个部分,面积分别为S1,S2,S3,S4.请直接写出含有S1,S2,S3,S4的一个等式.


 =
= S△ABC,请证明.
S△ABC,请证明. 与S四边形ABCD之间的数量关系.
与S四边形ABCD之间的数量关系.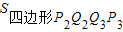 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com