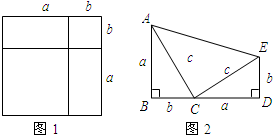（1）如图1是一个重要公式的几何解释，请你写出这个公式______；在推得这个公式的过程中，主要运用了______
A．分类讨论思想　　 B．整体思想　　 C．数形结合思想　　　D．转化思想
（2）如图2，Rt△ABC≌Rt△CDE，∠B=∠D=90°，且B，C，D在同一直线上．
求证：∠ACE=90°；
（3）伽菲尔德（1881年任美国第20届总统）利用（1）中的公式和图2证明了勾股定理（发表在1876年4月1日的《新英格兰教育日志》上），请你尝试该证明过程．

勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为（　　）

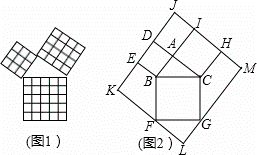
　　A．90　　B．100　　C．110　　D．121