
题目列表(包括答案和解析)
 ,那么至少应该放几个点
,那么至少应该放几个点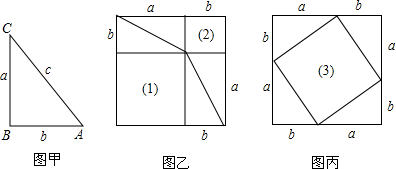
下图甲是任意一个直角三角形ABC,它的两条直角边的边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.
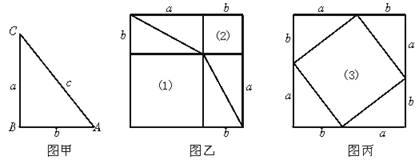
①图乙和图丙中(1)(2)(3)是否为正方形?为什么?
②图中(1)(2)(3)的面积分别是多少?
③图中(1)(2)的面积之和是多少?
④图中(1)(2)的面积之和与正方形(3)的面积有什么关系?为什么?
由此你能得到关于直角三角形三边长的关系吗?

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com