
题目列表(包括答案和解析)
如图,给你一张矩形纸,只用双手,你能折出一个等边三角形吗?
按下列步骤,如下图乙所示:
第一步:把矩形ABCD纸沿AB及CD的中点的连线对折,设折痕为EF;
第二步:过点B折叠,使A点落在折痕EF上,得到折痕BM
第三步:沿着MA线折叠,得到折痕MN.
请你说明△BMN是等边三角形.

 ,且tan∠DAF=
,且tan∠DAF= ,求矩形ABCD的周长;
,求矩形ABCD的周长;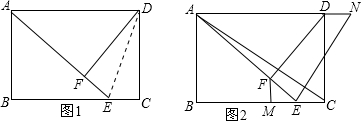
 如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD边上,将纸片沿BE折叠,使点A落在CD边上的F处.下列结论中:
如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD边上,将纸片沿BE折叠,使点A落在CD边上的F处.下列结论中:| 4 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
| 10 |
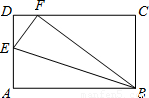 如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD边上,将纸片沿BE折叠,使点A落在CD边上的F处.下列结论中:
如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD边上,将纸片沿BE折叠,使点A落在CD边上的F处.下列结论中: ;②tan∠EBF=
;②tan∠EBF= ;③四边形ABFE的面积是矩形ABCD的面积的一半;④若在折痕BE上有点Q,使得△BFQ为等腰三角形,则EQ必然为
;③四边形ABFE的面积是矩形ABCD的面积的一半;④若在折痕BE上有点Q,使得△BFQ为等腰三角形,则EQ必然为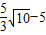 ;⑤若在折痕BE上有点P到边CD的距离与到点A的距离相等,则此相等距离为1.8.以上结论一定正确的个数为( )
;⑤若在折痕BE上有点P到边CD的距离与到点A的距离相等,则此相等距离为1.8.以上结论一定正确的个数为( ) 如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD边上,将纸片沿BE折叠,使点A落在CD边上的F处.下列结论中:
如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD边上,将纸片沿BE折叠,使点A落在CD边上的F处.下列结论中: ;②tan∠EBF=
;②tan∠EBF= ;③四边形ABFE的面积是矩形ABCD的面积的一半;④若在折痕BE上有点Q,使得△BFQ为等腰三角形,则EQ必然为
;③四边形ABFE的面积是矩形ABCD的面积的一半;④若在折痕BE上有点Q,使得△BFQ为等腰三角形,则EQ必然为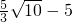 ;⑤若在折痕BE上有点P到边CD的距离与到点A的距离相等,则此相等距离为1.8.以上结论一定正确的个数为
;⑤若在折痕BE上有点P到边CD的距离与到点A的距离相等,则此相等距离为1.8.以上结论一定正确的个数为湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com