16、在等腰△ABC中，AB=AC．
（1）若M是BC的中点，过M任作一直线交AB，AC（或其延长线）于D，E，求证：2AB＜AD+AE．
（2）若P是△ABC内一点，且PB＜PC，求证：∠APB＞∠APC．

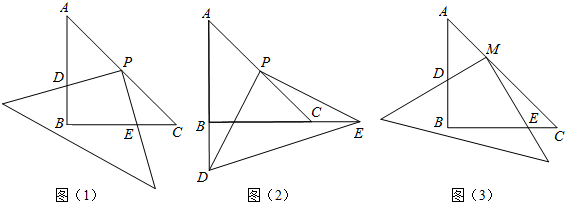
（2012•长宁区二模）在Rt△ABC中，AB=BC=4，∠B=90°，将一直角三角板的直角顶点放在斜边AC的中点P处，将三角板绕点P旋转，三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点（假设三角板的两直角边足够长），如图（1）、图（2）表示三角板旋转过程中的两种情形．
（1）直角三角板绕点P旋转过程中，当BE=时，△PEC是等腰三角形；
（2）直角三角板绕点P旋转到图（1）的情形时，求证：PD=PE；
（3）如图（3），若将直角三角板的直角顶点放在斜边AC的点M处，设AM：MC=m：n（m、n为正数），试判断MD、ME的数量关系，并说明理由．