三等分角仪－把材料制成如图所示的阴影部分的形状，使AB与半圆的半径CB、CD相等，PB垂直于AD．这便做成了“三等分角仪”．如果要把∠MPN三等分时，可将三等分角仪放在∠MPN上，适当调整它的位置，使PB通过角的顶点P，使A点落在角的PM边上，使角的另一边与半圆相切于E点，最后通过B、C两点分别作两条射线PB、PC，则∠MPB＝∠BPC＝∠CPN．请用推理的方法加以证明．

如图，直线y＝6－x交x轴、y轴于A、B两点，P是反比例函数图象上位于直线下方的一点，过点P作x轴的垂线，垂足为点M，交AB于点E，过点P作y轴的垂线，垂足为点N，交AB于点F．则AF·BE＝

A．8

B．6

C．4

D．

先阅读下面一段材料，再完成后面的问题：

材料　过抛物线y＝ax²(a＞0)的对称轴上一点(0，－)，作对称轴的垂线l，则抛物线上任意一点P到点F(0，)的距离与P到l的距离一定相等，我们将点F与直线l分别称作这抛物线的焦点和准线，如y＝x²的焦点为(0，)．

问题　若直线y＝kx＋b交抛物线y＝x²于A、B两点，AC、BD垂直于抛物线的准线l，垂直足分别为C、D(如图)．

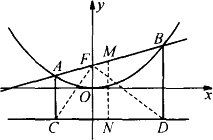
(1)求抛物线y＝x²的焦点F的坐标；

(2)求证：直线AB过焦点时，CF⊥DF；

(3)当直线AB过点(－1，0)，且以线段AB为直径的圆与准线l相切时，求这条直线对应的函数解析式．

已知，如图一条抛物线的对称轴是直线x＝，经过点(1，－3)、(3，－2)，与x轴交于A、B两点，与y轴交于点C．D、E分别是边AC、BC上的两个动点(不与A、B重合)，且保持DE∥AB．以DE为边向上作正方形DEFG．

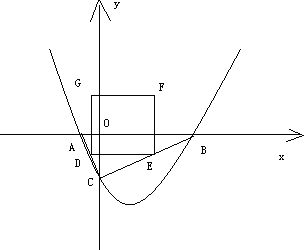
(1)求二次函数的解析式．

(2)试判断△ABC的形状，并说明理由．