
题目列表(包括答案和解析)
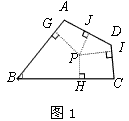
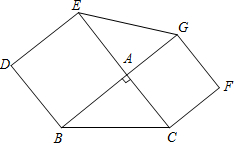
 定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,PH=PJ,PI=PG,,则点
定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,PH=PJ,PI=PG,,则点![]() 就是四边形ABCD的准内点.
就是四边形ABCD的准内点.
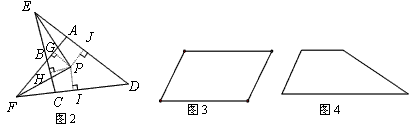
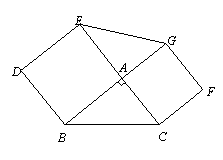
(1)如图2,∠AFD与∠DEC的角平分线FP,EP相交于点P.
求证:点P是四边形ABCD的准内点.
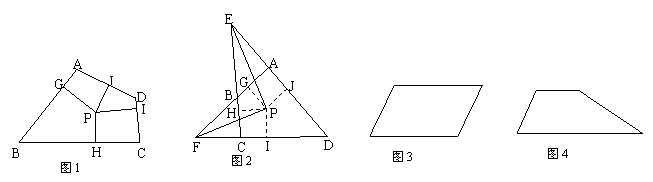
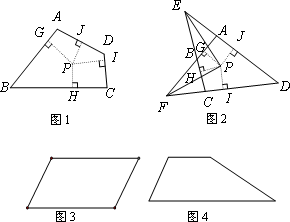
(2)分别画出图3平行四边形和图4梯形的准内点.(作图工具不限,不写作法,但要有必要的说明)
(3)判断下列命题的真假,在括号内填“真”或“假”.
①任意凸四边形一定存在准内点. ( )
②任意凸四边形一定只有一个准内点. ( )
③若P是任意凸四边形ABCD的准内点,则PA+PB=PC+PD或PA+PC=PB+PD. ( )
定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,PH=PJ,PI=PG,则点P就是四边形ABCD的准内点.
(1)如图2,∠AFD与∠DEC的角平分线FP,EP相交于点P.
求证:点P是四边形ABCD的准内点.
(2)分别画出图3平行四边形和图4梯形的准内点.(作图工具不限,不写作法,但要有必要的说明)
(3)判断下列命题的真假,在括号内填“真”或“假”.
①任意凸四边形一定存在准内点.( )
②任意凸四边形一定只有一个准内点.( )
③若P是任意凸四边形ABCD的准内点,则PA+PB=PC+PD或PA+PC=PB+PD.( )
 提出问题:
提出问题: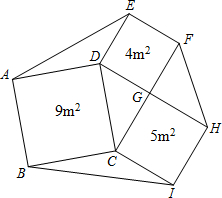 ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.提出问题
如图,在△ABC中,∠A=90°,分别以边AB、AC向外作正方形ABDE 和正方形 ACFG,连接EG,小亮发现△ABC与△AEG面积相等.小亮思考:这个问题中,如果∠A≠90°,那么△ABC与△AEG面积是否仍然相等?
猜想结论
经过研究,小亮认为:上述问题中,对于任意△ABC,分别以边AB、AC向外作正方形ABDE 和正方形 ACFG,连接EG,那么△ABC与△AEG面积相等.
证明猜想
(1)请你帮助小亮画出图形,并完成证明过程.已知:以△ABC的两边AB、AC为边长分别向外作正方形ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
结论应用
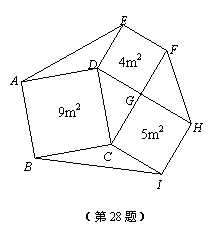
(2)学校教学楼前的一个六边形花圃被分成七个部分,分别种上不同品种的花卉,其中四边形ABCD、CIHG、GFED均为正方形,且面积分别为9m2、5m2和4m2.求这个六边形花圃ABIHFE的面积.
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com