
题目列表(包括答案和解析)
已知:下列图形都是由多个边长为1的正方形并排拼成的矩形.

(1)如图a所示,可以算出一个正方形的对角线长为![]() ,求两个正方形并排拼成的矩形的对角线长.n个呢?
,求两个正方形并排拼成的矩形的对角线长.n个呢?
(2)根据图b所示,求证:△BCE∽△BED;
(3)如图c所示,在下列所给的三个结论中,通过合情推理选出一个正确的结论加以证明:
①∠BEC+∠BDE=![]() ;
;
②∠BEC+∠BED=![]() ;
;
③∠BEC+∠DFE=![]() ;
;
(4)在图c中不添加辅助线和其他字母,你能否发现新的结论,如能,请加以证明.
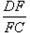 =
=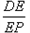 ,因为DE=EP,所以DF=FC,可求出EF和EG 的值,进而可求得EM与EN的比值.
,因为DE=EP,所以DF=FC,可求出EF和EG 的值,进而可求得EM与EN的比值. 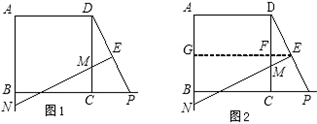
(8分)
数学课上,李老师出示了这样一道题目:如图![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,
,![]() 为边
为边![]() 延长线上的一点,
延长线上的一点,![]() 为
为![]() 的中点,
的中点,![]() 的垂直平分线交边
的垂直平分线交边![]() 于
于![]() ,交边
,交边![]() 的延长线于
的延长线于![]() .当
.当![]() 时,
时,![]() 与
与![]() 的比值是多少?
的比值是多少?
经过思考,小明展示了一种正确的解题思路:过![]() 作直线平行于
作直线平行于![]() 交
交![]() ,
,![]() 分别于
分别于![]() ,
,![]() ,如图
,如图![]() ,则可得:
,则可得:![]() ,因为
,因为![]() ,所以
,所以![]() .可求出
.可求出![]() 和
和![]() 的值,进而可求得
的值,进而可求得![]() 与
与![]() 的比值.
的比值.
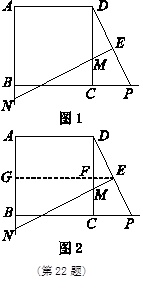
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了![]() 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
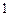 ,正方形
,正方形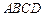 的边长为
的边长为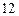 ,
,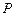 为边
为边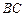 延长线上的一点,
延长线上的一点,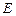 为
为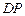 的中点,
的中点,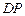 的垂直平分线交边
的垂直平分线交边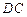 于
于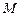 ,交边
,交边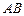 的延长线于
的延长线于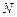 .当
.当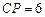 时,
时, 与
与 的比值是多少?
的比值是多少?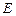 作直线平行于
作直线平行于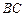 交
交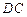 ,
,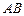 分别于
分别于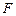 ,
,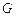 ,如图
,如图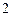 ,则可得:
,则可得: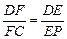 ,因为
,因为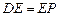 ,所以
,所以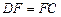 .可求出
.可求出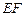 和
和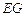 的值,进而可求得
的值,进而可求得 与
与 的比值.
的比值.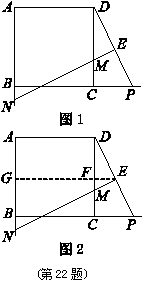
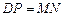 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.(8分)
数学课上,李老师出示了这样一道题目:如图 ,正方形
,正方形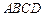 的边长为
的边长为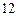 ,
, 为边
为边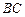 延长线上的一点,
延长线上的一点,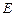 为
为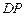 的中点,
的中点,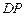 的垂直平分线交边
的垂直平分线交边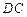 于
于 ,交边
,交边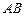 的延长线于
的延长线于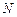 .当
.当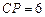 时,
时,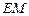 与
与 的比值是多少?
的比值是多少?
经过思考,小明展示了一种正确的解题思路:过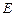 作直线平行于
作直线平行于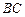 交
交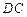 ,
,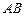 分别于
分别于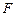 ,
,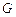 ,如图
,如图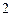 ,则可得:
,则可得: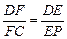 ,因为
,因为 ,所以
,所以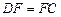 .可求出
.可求出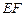 和
和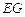 的值,进而可求得
的值,进而可求得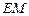 与
与 的比值.
的比值.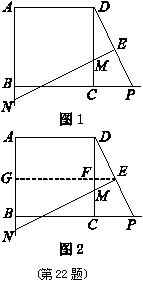
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了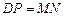 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com