
题目列表(包括答案和解析)
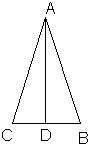 22、我们知道一个图形的性质和判定之间有着密切的联系.比如,由等腰三角形的性质“等边对等角”很易得到它的判定“等角对等边”.小明在学完“等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合”性质后,得到如下三个猜想:
22、我们知道一个图形的性质和判定之间有着密切的联系.比如,由等腰三角形的性质“等边对等角”很易得到它的判定“等角对等边”.小明在学完“等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合”性质后,得到如下三个猜想: 我们知道一个图形的性质和判定之间有着密切的联系.比如,由等腰三角形的性质“等边对等角”很易得到它的判定“等角对等边”.小明在学完“等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合”性质后,得到如下三个猜想:
我们知道一个图形的性质和判定之间有着密切的联系.比如,由等腰三角形的性质“等边对等角”很易得到它的判定“等角对等边”.小明在学完“等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合”性质后,得到如下三个猜想:
| 3 | x |
如图所示,![]() D,E为垂足,根据角平分线的性质和判定填空:
D,E为垂足,根据角平分线的性质和判定填空:

(1)若CD=CE,则有______;
(2)若∠1=∠2,则有______.
| |||||||||||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com