
题目列表(包括答案和解析)
用反证法证明命题“等角的补角相等”的第一步是:
________.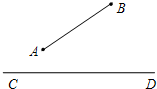 如图,光明乡的A、B两个村庄在河CD的同侧,两村庄的距离为
如图,光明乡的A、B两个村庄在河CD的同侧,两村庄的距离为| 13 |


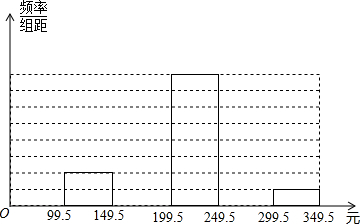 捐款,下面是对全校20个班捐款情况进行统计得到的频率分布表和频率分布直方图(部分).
捐款,下面是对全校20个班捐款情况进行统计得到的频率分布表和频率分布直方图(部分).| 分组 | 频数 | 频率 |
| 99.5~149.5 | 2 | 0.1 |
| 149.5~199.5 | 0.2 | |
| 199.5~249.5 | 8 | |
| 249.5~299.5 | 0.25 | |
| 299.5~349.5 | 1 | 0.05 |
| 合计 | 20 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com