
题目列表(包括答案和解析)
由四个完全相同的直角三角形拼得一个大正方形,如图所示.已知直角三角形两条直角边分别是7厘米和5厘米,求大正方形和小正方形的面积.(用两种方法解答)
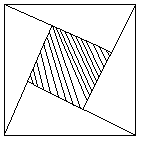
由四个完全相同的直角三角形拼得一个大正方形,如图已知直角三角形两条直角边分别是6cm、8cm,求大正方形的面积.(用两种方法解)

感知:利用图形中面积的等量关系可以得到某些数学公式.例如,根据图①甲,我们可以得到两数和的平方公式: ,根据图①乙能得到的数学公式是 .
,根据图①乙能得到的数学公式是 .
拓展:图②是由四个完全相同的直角三角形拼成的一个大正方形,直角三角形的两直角边长为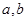 ,
, ,斜边长为
,斜边长为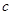 ,利用图②中的面积的等量关系可以得到直角三角形的三边长之间的一个重要公式,这个公式是: ,这就是著名的勾股定理.请利用图②证明勾股定理.
,利用图②中的面积的等量关系可以得到直角三角形的三边长之间的一个重要公式,这个公式是: ,这就是著名的勾股定理.请利用图②证明勾股定理.
应用:我国古代数学家赵爽的“勾股圆方图”是由四个完全相同的直角三角形与中间的一个小正方形拼成一个大正方形(如图③所示).如果大正方形的面积是17,小正方形的面积是1,直角三角形的两直角边长分别为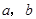 ,那么
,那么 的值是 .
的值是 .
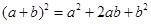 ,根据图①乙能得到的数学公式是 .
,根据图①乙能得到的数学公式是 .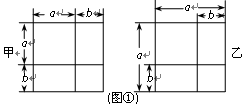
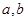 ,
,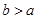 ,斜边长为
,斜边长为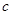 ,利用图②中的面积的等量关系可以得到直角三角形的三边长之间的一个重要公式,这个公式是: ,这就是著名的勾股定理.请利用图②证明勾股定理.
,利用图②中的面积的等量关系可以得到直角三角形的三边长之间的一个重要公式,这个公式是: ,这就是著名的勾股定理.请利用图②证明勾股定理.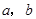 ,那么
,那么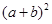 的值是 .
的值是 .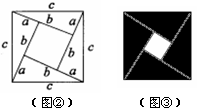
1.从不同角度计算图中边长为c的正方形的面积,你得到了什么?发现了什么?与勾股定理有关吗?试试看.
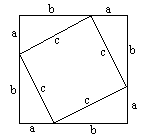
2.观察勾股定理a2+b2=c2中的c2、a2和b2,你想到了什么?
3.利用上图中四个完全相同的直角三角形,你还能拼出与c2有关的图形吗?能利用这个图形验证勾股定理吗?
4.用上图中的四个完全相同的直角三角形可以拼成如图Ⅰ所示的图形,这个图形被称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的.观察图Ⅰ,你能验证c2=a2+b2吗?把你的验证过程写下来,并与同伴进行交流.

2002年世界数学家大会(ICM-2002)在北京召开.图Ⅱ是此届大会的会标,其中央图案正是经过艺术处理的“弦图”.它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎来自世界各地的数学家们.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com