
题目列表(包括答案和解析)
| 已知:∠AOB=90。,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E。 (1)当三角板绕点C旋转到CD与OA垂直,CE与OB垂直时,(如图1) 此时由角平分线的性质可知CE=CD,又∵OM平分直角AOB,∴∠DOC=∠EOC=45。,∴△DCO与△ECO都为等腰直角三角形。∴OE=CE, OD=CD,又∵CE=CD,∴OE=OD=CD,请在此基础上继续证明: 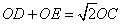 。 。(2)当三角板绕点C旋转到CD与OA不垂直时(如图2),上述结论是否还成立?试说明理由。 (3)当三角板绕点C旋转到图3位置上时,上述结论还成立吗?若不成立,请写出线段OD, OE, OC之间的关系。 |
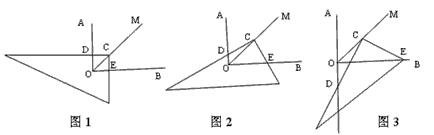 |
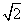 OC。当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明。
OC。当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明。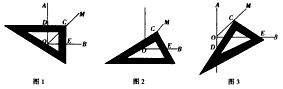
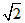 OC,
OC,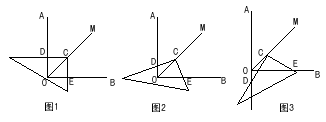
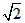 OC;
OC;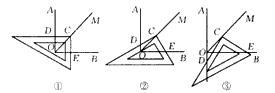
小明既无圆规,又无量角器,只有一个三角板,他是怎样画角平分线的呢?他的具体做法如下:在已知∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线交点为P,画射线OP.则OP平分∠AOB。其中运用的数学道理是 。 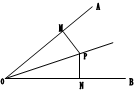
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com