
题目列表(包括答案和解析)
 ,过正方形的顶点A和对角线交点O作⊙O′,分别交AB、AD
,过正方形的顶点A和对角线交点O作⊙O′,分别交AB、AD 于F、E,⊙O′的半径为
于F、E,⊙O′的半径为 .
. 的值不变.其中只有一个结论是正确的,请选择正确的结论并求其值.
的值不变.其中只有一个结论是正确的,请选择正确的结论并求其值. ,过正方形的顶点A和对角线交点O作⊙O′,分别交AB、AD于F、E,⊙O′的半径为
,过正方形的顶点A和对角线交点O作⊙O′,分别交AB、AD于F、E,⊙O′的半径为 .
. 的值不变.其中只有一个结论是正确的,请选择正确的结论并求其值.
的值不变.其中只有一个结论是正确的,请选择正确的结论并求其值.
| 2 |
 于F、E,⊙O′的半径为
于F、E,⊙O′的半径为
| ||
| 2 |
| AE |
| AF |
问题背景:已知x是实数,求![]() 的最小值。要解决这个问题需现判断出0<x<12,继而联想到构造以边长为2+3和12为边的矩形,找出等于
的最小值。要解决这个问题需现判断出0<x<12,继而联想到构造以边长为2+3和12为边的矩形,找出等于![]() 的线段,再比较
的线段,再比较![]() 和矩形对角线的大小。
和矩形对角线的大小。
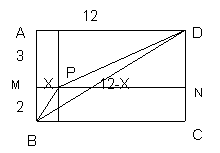 解:构造矩形ABCD,使AB=5,AD=12.在AB上截取AM=3,做矩形AMND。设点P是MN上一点MP=x,则PN=12-x,
解:构造矩形ABCD,使AB=5,AD=12.在AB上截取AM=3,做矩形AMND。设点P是MN上一点MP=x,则PN=12-x,

(1) 我们把上述求最值问题的方法叫做构图法.请仿造上述方法求![]() 的最小值。
的最小值。
探索创新:
(2)已知a,b,c,d是正实数且a+b+c+d=1,试运用构图法求![]() 的最小值.
的最小值.
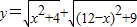 的最小值.要解决这个问题需现判断出0<x<12,继而联想到构造以边长为2+3和12为边的矩形,找出等于
的最小值.要解决这个问题需现判断出0<x<12,继而联想到构造以边长为2+3和12为边的矩形,找出等于 的线段,再比较
的线段,再比较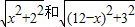 和矩形对角线的大小.
和矩形对角线的大小.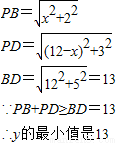
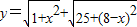 的最小值.
的最小值.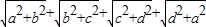 的最小值.
的最小值.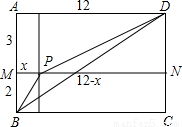
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com