在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色的纸边，制成一幅矩形挂图．如图所示，如果要使整个挂图的面积是5400cm²，则金色的纸边的宽为多少cm？

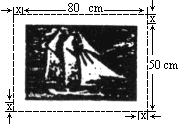
(1)如果列方程解决这一实际问题，则相等关系怎样，请表示出来．

(2)如果设金色纸边的边宽为xcm，那么这幅矩形挂图的长为________cm，宽为________cm．

(3)可列出方程：________．

(4)x＝－70和x＝5是(3)中的方程的解吗？试一试，并判断符合实际意义的解是哪一个？

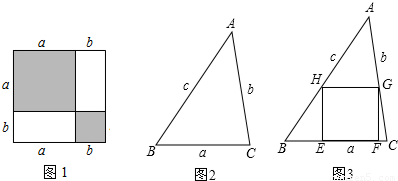
如图①，△ABD是直角三角形，∠C＝，现将△ABC补成矩形，使△ABC的两个顶点为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上，则符合要求的矩形可以画出两个：矩形ACBD和矩形AEFB(如图②)．

解答问题：

(1)设图②中矩形ACBD和矩形AEFB的面积分别为S₁，S₂，则S₁_______S₂．(填“＞”、“＝”或“＜”)

(2)如图③，△ABC是钝角三角形，按题设要求把它补成矩形，那么符合要求的矩形可以画出_______个．

(3)如图④，△ABC是锐角三角形，且三边满足BC＞AC＞AB，按题设要求把它补成矩形，那么符合要求的矩形可以画出_______个．

(4)在(3)中所画出的矩形中，哪一个的周长最小？为什么？

阅读下面短文：如图（A）DABC是直角三角形，ÐC=90°，现将DABC补成矩形，使DABC的两个顶点为矩形的两个顶点，另一个顶点在矩形上，可以画出两个矩形ACBD和矩形AEFB。

解答问题：

（1）设图（B）中矩形ACBD和矩形AEFB的面积分别为S₁、S₂，则S₁________S₂。（填>，<或=）

（2）如下图（A），DABC是钝角三角形，按短文中的要求把它补成矩形，那么符合要求的矩形可以画出________个，利用下图（A）把它画出来。

（3）如下图（B），DABC是锐角三角形且三边满足BC>AC>AB，按短文中的要求把它补成矩形，那么符合要求的矩形可以画出________个，利用下图（B）把它画出来。