（本小题满分14分）如图9，在直角坐标系xoy中，O是坐标原点，点A在x正半轴上，OA=cm，点B在y轴的正半轴上，OB=12cm，动点P从点O开始沿OA以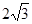cm/s的速度向点A移动，动点Q从点A开始沿AB以4cm/s的速度向点B移动，动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动，移动时间为t（0＜t＜6）s.

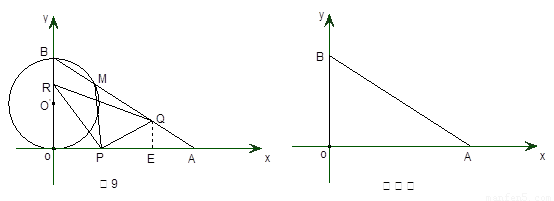
（1）求∠OAB的度数.

（2）以OB为直径的⊙O‘与AB交于点M，当t为何值时，PM与⊙O‘相切？

（3）写出△PQR的面积S随动点移动时间t的函数关系式，并求s的最小值及相应的t值.

（4）是否存在△APQ为等腰三角形，若存在，求出相应的t值，若不存在请说明理由.

（本小题满分14分）

已知：如图，抛物线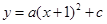与y轴交于点C（0，），  与x轴交于点A、 B，点A的坐标为（2，0）．

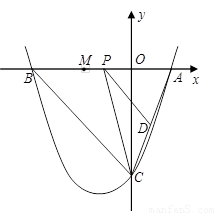
（1）求该抛物线的解析式；

（2）点P是线段AB上的动点，过点P作PD∥BC，交AC于点D，连接CP．当△CPD的面积最大时，求点P的坐标；

（3）若平行于x轴的动直线与该抛物线交于点Q，与直线BC交于点F，点M 的坐标为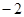（，0）．问：是否存在这样的直线，使得△OMF是等腰三角形？若存   在，请求出点Q的坐标；若不存在，请说明理由．

（本小题满分5分）某校对九年级学生进行“综合素质”评价，评价的结果为A（优）、B（良好）、C(合格)、D(不合格)四个等级，现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理，并作出如图所示的统计图，已知图中从左到右的四个长方形的高的比为：14：9：6：1，评价结果为D等级的有2人，请你回答以下问题：

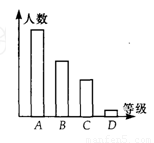
1. (1)共抽测了多少人？

2. (2)样本中B等级的频率是多少？

3.(3) 如果要绘制扇形统计图，A等级在扇形统计图中所占的圆心角是多少度？

4.(4)该校九年级的毕业生共300人，假如“综合素质”等级为A或B的学生才能报考示范性高中，请你计算该校大约有多少名学生可以报考示范性高中？

25.（本小题满分14分）

如图13，二次函数的图象与x轴交于A、B两点，与y轴交于点C（0，-1），ΔABC的面积为。

（1）求该二次函数的关系式；

（2）过y轴上的一点M（0，m）作y轴上午垂线，若该垂线与ΔABC的外接圆有公共点，求m的取值范围；

（3）在该二次函数的图象上是否存在点D，使四边形ABCD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由。

（本小题满分10分）

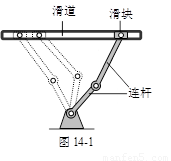
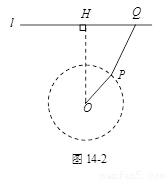
观察思考

某种在同一平面进行传动的机械装置如图14-1，图14-2是它的示意图．其工作原理是：滑块Q在平直滑道l上可以左右滑动，在Q滑动的过程中，连杆PQ也随之运动，并且PQ带动连杆OP绕固定点O摆动．在摆动过程中，两连杆的接点P在以OP为半径的⊙O上运动．数学兴趣小组为进一步研究其中所蕴含的数学知识，过点O作OH ⊥l于点H，并测得OH = 4分米，PQ = 3分米，OP = 2分米．

解决问题

（1）点Q与点O间的最小距离是        分米；点Q与点O间的最大距离是        分米；点Q在l上滑到最左端的位置与滑到最右端位置间的距离是        分米．

（2）

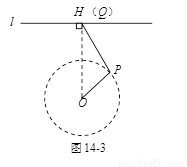
如图14-3，小明同学说：“当点Q滑动到点H的位置时，PQ与⊙O是相切的．”你认为他的判断对吗？为什么？

（3）①小丽同学发现：“当点P运动到OH上时，点P到l的距离最小．”事实上，还存在着点P到l距离最大的位置，此时，点P到l的距离是        分米；

②当OP绕点O左右摆动时，所扫过的区域为扇形，求这个扇形面积最大时圆心角的度数．