
题目列表(包括答案和解析)
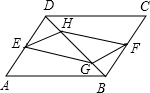 如图,已知:在?ABCD中,E、F分别是AD、BC边的中点,G、H是对角线BD上的两点,且BG=DH,则下列结论中不正确的是( )
如图,已知:在?ABCD中,E、F分别是AD、BC边的中点,G、H是对角线BD上的两点,且BG=DH,则下列结论中不正确的是( )| A、GF⊥FH | B、GF=EH | C、EF与AC互相平分 | D、EG=FH |
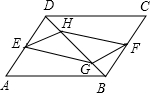 如图,已知:在?ABCD中,E、F分别是AD、BC边的中点,G、H是对角线BD上的两点,且BG=DH,则下列结论中不正确的是
如图,已知:在?ABCD中,E、F分别是AD、BC边的中点,G、H是对角线BD上的两点,且BG=DH,则下列结论中不正确的是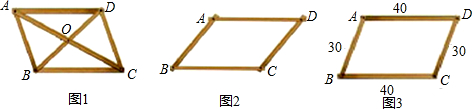

 ,
,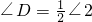 .∵∠1+∠2=360°∴
.∵∠1+∠2=360°∴ ,同理∠BAD+∠BCD=180°,即圆内接四边形对角(相对的两个角)互补.
,同理∠BAD+∠BCD=180°,即圆内接四边形对角(相对的两个角)互补.
我们学习了菱形,知道菱形的面积计算有一个比较特殊的方法,就是S菱形等于对角线乘积的一半.其实不仅菱形是这样的,只要对角线互相垂直的四边形面积均等于对角线乘积的一半,即S菱=![]() ab(其中a、b为两对角线的长度).
ab(其中a、b为两对角线的长度).
证明如下:如图,在四边形ABCD中,对角线AC⊥BD,垂足为P.求证:S四边形ABCD=![]() AC·BD.
AC·BD.

证明:

解答问题:
(1)上述证明得到的性质可叙述为:________.
(2)已知:如图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD,且相交于点P,AD=3 cm,BC=7 cm,利用上述性质求梯形的面积.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com