
题目列表(包括答案和解析)




探索、研究:下图是按照一定的规律画出的一列“树型”图,下表的n表示“树型”图的序号,an表示第n个“树型”图中“树枝”的个数。
图:
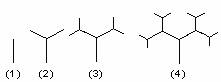
| n | 1 | 2 | 3 | 4 | … |
| an | 1 | 3 | 7 | 15 | … |
表:
⑴ 根据“图”、“表”可以归纳出an关于n的关系式为____________________。
若直线![]() 经过点
经过点![]() 、
、![]() ,求直线
,求直线![]() 对应的函数关系式,并说明对任意的正整数n,点
对应的函数关系式,并说明对任意的正整数n,点![]() 都在直线
都在直线![]() 上。
上。
⑵ 设直线![]() :
:![]() 与x轴相交于点A,与直线
与x轴相交于点A,与直线![]() 相交于点M,双曲线
相交于点M,双曲线![]() 经过点M,且与直线
经过点M,且与直线![]() 相交于另一点N。
相交于另一点N。
① 求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线![]() 、
、![]() 。
。
② 设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为![]() ,直线MP与x轴相交于点Q,当
,直线MP与x轴相交于点Q,当![]() 为何值时,
为何值时,![]() 的面积等于
的面积等于![]() 的面积的2倍?又是否存在
的面积的2倍?又是否存在![]() 的值,使得
的值,使得![]() 的面积等于1?若存在,求出
的面积等于1?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
③ 在y轴上是否存在点G,使得![]() 的周长最小?若存在,求出点G的坐标;若不存在,请说明理由。
的周长最小?若存在,求出点G的坐标;若不存在,请说明理由。
【答案】1.1×107。
【考点】科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】将11000000用科学记数法表示为:1.1×107.
故答案为:1.1×107.
【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
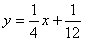 的图象上的点,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)(n是正整数)依次是x轴正半轴上的点,已知x1=a(0<a<1),△A1B1A2,△A2B2A3,△A3B3A4…△AnBnAn+1分别是以B1,B2,B3,…,Bn为顶点的等腰三角形。
的图象上的点,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)(n是正整数)依次是x轴正半轴上的点,已知x1=a(0<a<1),△A1B1A2,△A2B2A3,△A3B3A4…△AnBnAn+1分别是以B1,B2,B3,…,Bn为顶点的等腰三角形。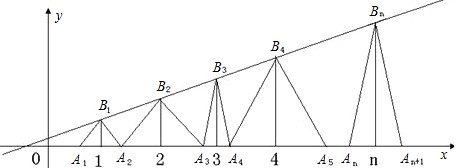

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com