
题目列表(包括答案和解析)

 (2012•浦口区一模)提出问题:
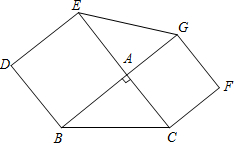
(2012•浦口区一模)提出问题: ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.学习了“多边形内角和”这一节后,老师给茗茗留了一道习题,请你帮茗茗完成.
(1)①如图19-1,在△ABC中,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2的度数为 ;②如图19-2,在△ABC中,∠A=50°,剪去∠A后成四边形,则∠1+∠2的度数为 ;③根据①与②的求解过程,请你猜想∠1+∠2与∠A的关系是 ;
(2)在(1)中可以知道,一个三角形,通过剪去一个角将它变成四边形时,所得到的新的角和被剪去角之间的关系,如果剪去三角形的两个角,将它变成一个五边形时,剪去的两个角和新的角之间又有怎样的关系?剪去三角形的三个角,将它变成一个六边形时,剪去的三个角和新的角之间又有怎样的关系?
(3)如果将四边形剪去一个角变成五边形,剪去两个角变成六边形,剪去三个角变成七边形,所剪去的角和新角的关系是否与(2)中的相同?如果不同,请说明理由.
 |
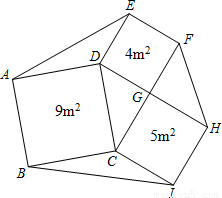
 提出问题:
提出问题: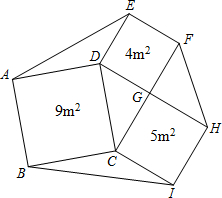 ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com