操作实验：

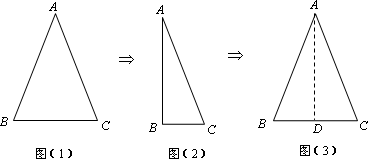
如图，把等腰三角形沿顶角平分线对折并展开，发现被折痕分成的两个三角形成轴对称．

所以△ABD≌△ACD，所以∠B＝∠C．

归纳结论：如果一个三角形有两条边相等，那么这两条边所对的角也相等．

根据上述内容，回答下列问题：

思考验证：

如图(4)，在△ABC中，AB＝AC．

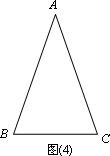
试说明∠B＝∠C的理由．(添加辅助线说明)

探究应用：

如图(5)，CB⊥AB，垂足为B，DA⊥AB，垂足为A．E为AB的中点，AB＝BC，CE⊥BD于F，连接DC、DE、AC，AC与DE交于点O．

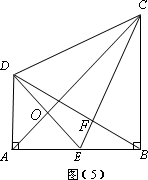
(1)BE与AD是否相等？为什么？

(2)小明认为AC垂直平分线段DE，你认为对吗？说说你的理由．

(3)∠DBC与∠DCB相等吗？试说明理由．

在△ABC中，AB＝AC，CG⊥BA交BA的延长线于点G．一等腰直角三角尺按如图1所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．

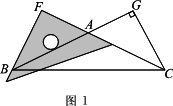
(1)在图1中请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想；

(2)当三角尺沿AC方向平移到图2所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E．此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE＋DF与CG之间满足的数量关系，然后证明你的猜想；

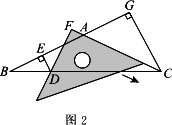
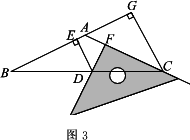
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上，且点F与点C不重合)时，(2)中的猜想是否仍然成立？(不用说明理由)