练习册

  • 练习册
  • 试题
    27．如图12.22.将△BMN以∠DMN的角平分线 为轴翻折至△PDM的位置.即取AD的中点P. 连结PM．从而△MPD≌△NBM.故DM=MN． 【查看更多】

     

    题目列表(包括答案和解析)

    18、将连续的自然数1至1001按如图的方式排列成一个长方形阵列，用一个正方形框出9个数，要使这个正方形框出的9个数之和分别为：（1）2007；（2）2008、这是否可能？若可能，请写出这9个数中的最小数和最大数；若不可能，试说明理由．
    1 2 3 4 5 6 7
    8 9 10 11 12 13 14
    15 16 17 18 19 20 21
    22 23 24 25 26 27 28
    … … … … … … …
    995 996 997 998 999 1000 1001

    查看答案和解析>>

    某汽车制造公司计划生产A、B、C三种型号的汽车共80辆．并且公司在设计上要求，A、C两种型号之间按如图所示的函数关系生产．该公司投入资金不少于1212万元，但不超过1224万元，且所有资金全部用于生产这三种型号的汽车，三种型号的汽车生产成本和售价如下表：
    A B C
    成本（万元/辆） 12 15 18
    售价（万元/辆） 14 18 22
    设A种型号的汽车生产x辆；
    （1）设C种型号的汽车生产y辆，求出y与x的函数关系式；
    （2）该公司对这三种型号汽车有哪几种生产方案？
    （3）设该公司卖车获得的利润W万元，求公司如何生产获得利润最大？
    （4）根据市场调查，每辆A、B型号汽车的售价不会改变，每辆C型号汽车在不亏本的情况下售价将会降价a万元（a＞0），且所生产的三种型号汽车可全部售出，该公司又将如何生产获得利润最大？（注：利润=售价-成本）

    查看答案和解析>>

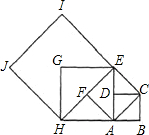    精英家教网阅读下面的文字，回答后面的问题．
    求3+32+33+…+3100的值．
    解：令S=3+32+33+…+3100（1），将等式两边提示乘以3得到：3S=32+33+34+…+3101（2），（2）-（1）得到：2S=3101-3
    ∴S=
    3101-32

    问题（1）求2+22+…+2100的值；
    （2）求4+12+36+…+4×340的值；
    （3）如图，设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第二个正方形AEGH，如此下去…一直作图到第10个图形为止．已知正方形ABCD的边长为1，求所有的正方形的所有边长之和．

    查看答案和解析>>

    如图1，⊙O的半径为1，AB为⊙O的直径，P为⊙O上一点．设∠POB为α（α为锐角），PC⊥AB于C．当α=60°、45°时，图2、图3中PC、OC、tan∠PAB的值分别见下表，
    α PC的值 OC的值 tan∠PAB的值
    α=60°
    		3
    2
    1
    2
    		 tan∠PAB=tan30°=
    		3
    3
    α=45°
    		2
    2
    		2
    2
    		 tan∠PAB=tan22.5°=
    		2
    -1
    α=30° tan∠PAB=tan15°=
     
    α tan∠PAB=tan
     
    =
     
    请根据图4、图1将表中空白处填写完整．
    精英家教网

    查看答案和解析>>

    （1）计算：-22+（tan60°-1）×
    		3
    +（-
    1
    2
    ）-2+（-π）0-|2-
    		3
    |；
    （2）先化简再求值(1+
    1
    x-2
    )÷
    x2-1
    2x-4
    ，其中x=3．
    （3）物理兴趣小组20位同学在实验操作中的得分情况如下表：精英家教网
    得分（分） 10 9 8 7
    人数（人） 5 8 4 3
    问：①求这20位同学实验操作得分的众数，中位数；
    ②这20位同学实验操作得分的平均分是多少？
    ③将此次操作得分按人数制成如图所示的扇形统计图．扇形①的圆心角度数是多少？

    查看答案和解析>>


    同步练习册答案