
题目列表(包括答案和解析)
先阅读,后解答下列题目:
甲数比乙数的一半少2,已知甲数等于3,求乙数.
解:设 乙数为x,根据题意,得![]() ,x=10.
,x=10.
象上面解题的思想方法,我们称之为方程思想,请用列方程的方法解答下题:
某学校七(5)班一部分同学进行个人投篮比赛,受污损的下表记录了在规定时间内投进n个球的人数分布情况:
|
进球数n |
0 |
1 |
2 |
3 |
4 |
5 |
|
投进n个球的人数 |
1 |
2 |
7 |
2 |
(1)同时,已知进3个球的人数是进4个球人数的3倍,并且进球3个或3个以上的人平均投进3.5个球,问投进3个球与4个球的人各有多少人?
(2
)根据题目,仿照(1),编一道应用题.
| |||||||
请同学们认真阅读下面材料,然后解答问题。(6分)
解方程(x2-1)2-5(x-1)+4=0
解:设y=x2-1
则原方程化为:y2-5y+4=0 ① ∴y1=1 y2=4
当y=1时,有x2-1=1,即x2=2 ∴x=±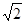
当y=4时,有x2-1=4,即x2=5
∴x=±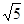
∴原方程的解为:x1=-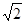 x2=
x2=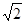 x3=-
x3=-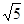 x4=
x4=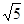
解答问题:
⑴填空:在由原方程得到①的过程中,利用________________法达到了降次的目的,体现了________________的数学思想。
⑵解方程 -3(
-3(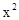 -3)=0
-3)=0
请同学们认真阅读下面材料,然后解答问题。(6分)
解方程(x2-1)2-5(x-1)+4=0
解:设y=x2-1
则原方程化为:y2-5y+4=0 ① ∴y1=1 y2=4
当y=1时,有x2-1=1,即x2=2 ∴x=±
当y=4时,有x2-1=4,即x2=5 ∴x=±
∴原方程的解为:x1=- x2=
x3=-
x4=
解答问题:
⑴填空:在由原方程得到①的过程中,利用________________法达到了降次的目的,体现了________________的数学思想。
⑵解方程-3(
-3)=0
请同学们认真阅读下面材料,然后解答问题。(6分)
解方程(x2-1)2-5(x-1)+4=0
解:设y=x2-1
则原方程化为:y2-5y+4=0 ① ∴y1=1 y2=4
当y=1时,有x2-1=1,即x2=2 ∴x=±
当y=4时,有x2-1=4,即x2=5 ∴x=±
∴原方程的解为:x1=- x2=
x2= x3=-
x3=- x4=
x4=
解答问题:
⑴填空:在由原方程得到①的过程中,利用________________法达到了降次的目的,体现了________________的数学思想。
⑵解方程 -3(
-3( -3)=0
-3)=0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com