
题目列表(包括答案和解析)
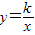 和
和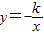 (k≠0)的图象关于y轴对称,我们把函数
(k≠0)的图象关于y轴对称,我们把函数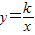 和
和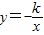 (k≠0)叫做互为“镜子”函数.类似地,如果函数y=f(x)和y=h(x)的图象关于y轴对称,那么我们就把函数y=f(x)和y=h(x)叫做互为“镜子”函数.
(k≠0)叫做互为“镜子”函数.类似地,如果函数y=f(x)和y=h(x)的图象关于y轴对称,那么我们就把函数y=f(x)和y=h(x)叫做互为“镜子”函数.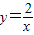 (x>0)和
(x>0)和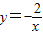 (x<0)的图象分别交于点A、B、C,如果CB:AB=1:2,点C在函数
(x<0)的图象分别交于点A、B、C,如果CB:AB=1:2,点C在函数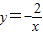 (x<0)的“镜子”函数上的对应点的横坐标是
(x<0)的“镜子”函数上的对应点的横坐标是 ,求点B的坐标.
,求点B的坐标.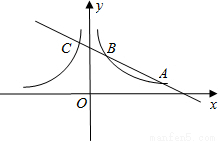
 和
和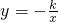 (k≠0)的图象关于y轴对称,我们把函数
(k≠0)的图象关于y轴对称,我们把函数 和
和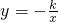 (k≠0)叫做互为“镜子”函数.类似地,如果函数y=f(x)和y=h(x)的图象关于y轴对称,那么我们就把函数y=f(x)和y=h(x)叫做互为“镜
(k≠0)叫做互为“镜子”函数.类似地,如果函数y=f(x)和y=h(x)的图象关于y轴对称,那么我们就把函数y=f(x)和y=h(x)叫做互为“镜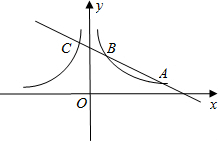 子”函数.
子”函数. (x>0)和
(x>0)和 (x<0)的图象分别交于点A、B、C,如果CB:AB=1:2,点C在函数
(x<0)的图象分别交于点A、B、C,如果CB:AB=1:2,点C在函数 (x<0)的“镜子”函数上的对应点的横坐标是
(x<0)的“镜子”函数上的对应点的横坐标是 ,求点B的坐标.
,求点B的坐标.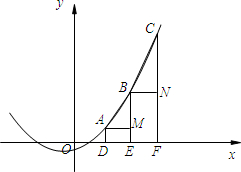 在函数中,我们规定:当自变量增加一个单位时,因变量的增加量称为函数的平均变化率.例如,对于函数y=3x+1,当自变量x增加1时,因变量y=3(x+1)+1=3x+4,较之前增加3,故函数y=3x+1的平均变化率为3.
在函数中,我们规定:当自变量增加一个单位时,因变量的增加量称为函数的平均变化率.例如,对于函数y=3x+1,当自变量x增加1时,因变量y=3(x+1)+1=3x+4,较之前增加3,故函数y=3x+1的平均变化率为3.
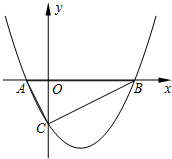 如图,二次函数y=a(x2-3x-4)(其中a>0)的图象与x轴交于A、B两点,与y轴交于C点,且tan∠BAC=2.
如图,二次函数y=a(x2-3x-4)(其中a>0)的图象与x轴交于A、B两点,与y轴交于C点,且tan∠BAC=2.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com