练习册

  • 练习册
  • 试题
    如图.将矩形纸片折叠.先折出折痕BD.再折使AD边与对角线BD重合.得折痕DG.若AB=2.BC=1.求AG的长. 【查看更多】

     

    题目列表(包括答案和解析)

    如图，将一张矩形纸片ABCD先折出一条对角线AC，再将点A与点C重合折出折痕EF，最后分别沿AE、CF折叠，得到的四边形AECF是什么样的四边形？试证明你的猜想。

    查看答案和解析>>

    (1)如图，折叠矩形纸片ABCD，先折出折痕(对角线)BD，再折叠，使AD落在对角线BD上，得折痕DG，若AB＝2，BC＝1，则AG＝________．

    (2)如图，将边长为1的正方形ABCD绕A点按逆时针方向旋转，至正方形，则旋转前后两个正方形重叠部分的面积是________．

    查看答案和解析>>

    小明取出一张矩形纸片ABCD，AD=BC=5，AB=CD=25．他先在矩形ABCD的边AB上取一点M，接着在CD上取一点N，然后将纸片沿MN折叠，使MB′与DN交于点K，得到△MNK（如图①）．
    （1）试判断△MNK的形状，并说明理由．
    （2）如何折叠能够使△MNK的面积最大？请你利用备用图探究可能出现的情况，求出最大值．

    查看答案和解析>>

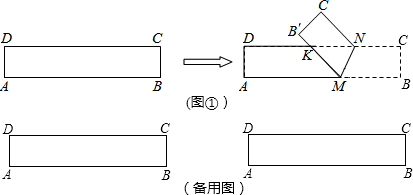
    如图①，四边形ABCD是一张矩形纸片，∠BAC＝α(0°＜α≤45°)，现将其折叠，使点A、C重合．

    (1)先用一张矩形纸片尝试折叠，并在图上画出折叠痕EF；

    (2)设AC＝x，EF＝y，求出y与x之间的函数关系式；

    (3)如图②，当45°＜α＜90°时，求得的函数关系式是否和①中求得的函数关系式相同？

    查看答案和解析>>

    24、小明打算用如图的矩形纸片ABCD折出一个等边三角形．他的操作步骤是：
    ①先把矩形纸片对折后展开，并设折痕为AM；
    ②把B点叠在折痕线上，得到Rt△AB1E；
    ③沿着EB1线折叠，得到△EAF．小明认为，所得的△EAF即为等边三角形．
    试问，小明的结论是否正确？若正确，请给予证明；若不正确，请你给出一种将矩形纸片ABCD折为一个等边三角形的方法．

    查看答案和解析>>


    同步练习册答案