
题目列表(包括答案和解析)
阅读以下的材料:
如果两个正数a,b,即a>0,b>0,有下面的不等式: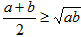 当且仅当a=b时取到等号
当且仅当a=b时取到等号
我们把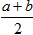 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把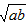 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
例:已知x>0,求函数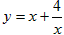 的最小值。
的最小值。
解:令a=x,b=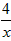 ,则有
,则有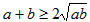 ,得
,得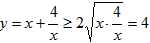 ,当且仅当
,当且仅当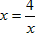 时,即x=2时,函数有最小值,最小值为2。
时,即x=2时,函数有最小值,最小值为2。
根据上面回答下列问题:
①已知x>0,则当x=____时,函数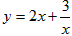 取到最小值,最小值为____;
取到最小值,最小值为____;
②用篱笆围一个面积为100m2的矩形花园,问这个矩形的长、宽各为多少时,所用的篱笆最短,最短的篱笆周长是多少;
③已知x>0,则自变量x取何值时,函数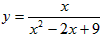 取到最大值,最大值为多少?
取到最大值,最大值为多少?
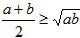 当且仅当a=b时取到等号,我们把
当且仅当a=b时取到等号,我们把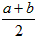 叫做正数的算术平均数,把
叫做正数的算术平均数,把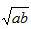 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子: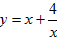 的最小值。
的最小值。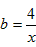 ,则有
,则有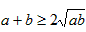 ,得
,得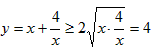 ,当且仅当
,当且仅当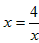 时,即x=2时,函数有最小值,最小值为2。
时,即x=2时,函数有最小值,最小值为2。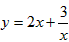 取到最小值,最小值为______;
取到最小值,最小值为______;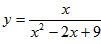 取到最大值,最大值为多少?
取到最大值,最大值为多少? 先阅读下列文字,再解答下列问题:
数学课本中有这样一段叙述:“要比较a与b的大小,可先求出a与b的差,再看这个差是正数、负数还是零。”由此可见,要判断两个代数式值的大小,只要考虑它们的差就可以了。
1.试问:甲乙两人两次同时在同一粮店购买粮食(假设两次购买粮食的单价不相同),甲每次购买粮食100千克,乙每次购粮用去100元。
(1)假设x、y分别表示两次购粮的单价(单位:元/千克),试用含x、y的代数式表示:
甲两次购买粮食共需付款____元;乙两次共购买____千克的粮食;
若甲两次购粮的平均单价为每千克Q1元,乙两次购粮的平均单价为每千克Q2元,则Q1=____;Q2=____
(2)规定:谁两次购粮的平均单价低,谁的购粮方式就更合算,请你判断甲乙两人的购粮方式哪一个更合算些?并说明理由;
2.已知a>b>0,c>0,你能根据前面阅读比较出 与
与 的大小吗?并说明理由.
的大小吗?并说明理由.
书本P58实验与探究中,介绍了三角形中边与角之间的不等关系,利用轴对称方法证明了:一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大。
下面用另外一种方法来证明这个结论。
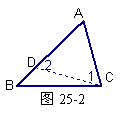
如图25-1,在⊿ABC中,AB>AC,求证:∠ACB>∠B
证明:如图25-2,在边AB截取一点D,使AD=AC, ∵AD=AC ∴∠1=∠2
∴∠ACB>∠1 又∵∠1=∠2 ∠2>∠B ∴∠ACB>∠B
利用上述结论或方法,解决下列问题:
(1)在⊿ABC中,已知BC>AB>AC,猜想∠A,∠B,∠C的大小关系是_________________
(2)已知:如图25-3,在⊿ABC中,∠ACB>∠B,求证:AB>AC
(3)如果一![]() 个三角形中最大的边所对的角是锐
个三角形中最大的边所对的角是锐![]() 角,这个三角形一定是锐角三角形吗?为什么?
角,这个三角形一定是锐角三角形吗?为什么?

 |

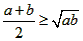 当且仅当a=b时取到等号,我们把
当且仅当a=b时取到等号,我们把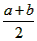 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把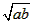 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子: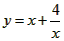 的最小值。
的最小值。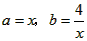 ,则有
,则有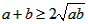 ,得
,得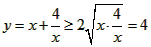 ,当且仅当
,当且仅当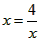 时,即时x=2,函数有最小值,最小值为2。
时,即时x=2,函数有最小值,最小值为2。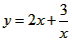 取到最小值,最小值为______;
取到最小值,最小值为______;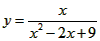 取到最大值,最大值为多少?
取到最大值,最大值为多少? 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com