
题目列表(包括答案和解析)
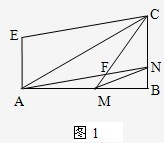
如图,△ABC为锐角三角形,向形外作正方形ACDE和正方形ABGF,连接FE,求证:S△AFE=S△ABC
证明:过点C作CM⊥AB于M,过点E作EN⊥FA交FA的延长线于N,
∴∠AMC=∠ANE=90°
∵ACDE是正方形 ∴AE=AC ∠EAC=90° ∴∠2+∠3=90°
又∵ABGF是正方形 ∴∠FAB=90° ∴∠BAN=90°
∴∠1+∠2=90° ∴∠1=∠3 ∴Rt△AMC≌Rt△ANE
∴CM=EN 又∵ABGF是正方形 ∴AF=AB
S△AFE=![]() AF?EN S△ABC=
AF?EN S△ABC=![]() AB?CM
AB?CM
∴S△AFE=S△ABC
请你再用另一种方法证明S△AFE=S△ABC.
(过点B作AC的垂线,过F点作AE的垂线与上面证法属同一种方法)


| 1 |
| 2 |
| k |
| x |

| k |
| x |
| 3 |
| 2 |
| EF |
| CD |
 | AB |
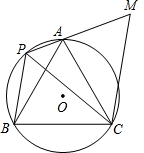 M∥BP交PA的延长线于点M.
M∥BP交PA的延长线于点M.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com