
题目列表(包括答案和解析)
数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答:
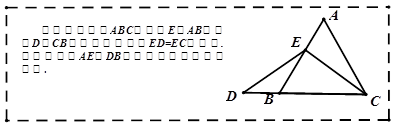
1.特殊情况,探索结论. 当点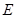 为
为![]() 的中点时,确定线段
的中点时,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:![]()
![]() (填“>”,“<”或“=”).
(填“>”,“<”或“=”).
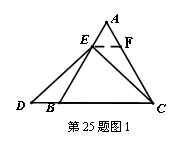
2.特例启发,解答题目
解:题目中,![]() 与
与![]() 的大小关系是:
的大小关系是:![]()
![]() (填“>”,“<”或“=”).理由如下:
(填“>”,“<”或“=”).理由如下:
如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .(请你完成以下解答过程)
.(请你完成以下解答过程)
3.拓展结论,设计新题
在等边三角形![]() 中,点
中,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() .若
.若![]() 的边长为1,
的边长为1,![]() ,则
,则![]() 的长为 (请你画出图形并直接写出结果,图没画或画错均不得分).
的长为 (请你画出图形并直接写出结果,图没画或画错均不得分).
数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答: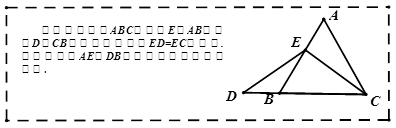
【小题1】特殊情况,探索结论. 当点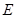 为
为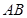 的中点时,确定线段
的中点时,确定线段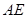 与
与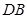 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论: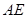
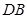 (填“>”,“<”或“=”).
(填“>”,“<”或“=”).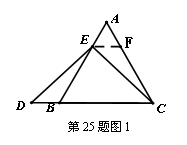
【小题2】特例启发,解答题目
解:题目中,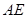 与
与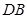 的大小关系是:
的大小关系是: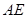
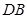 (填“>”,“<”或“=”).理由如下:
(填“>”,“<”或“=”).理由如下:
如图1,过点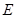 作
作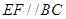 ,交
,交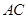 于点
于点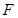 .(请你完成以下解答过程)
.(请你完成以下解答过程)
【小题3】拓展结论,设计新题
在等边三角形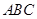 中,点
中,点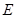 在直线
在直线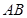 上,点
上,点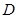 在直线
在直线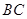 上,且
上,且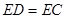 .若
.若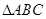 的边长为1,
的边长为1,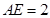 ,则
,则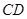 的长为 (请你画出图形并直接写出结果,图没画或画错均不得分).
的长为 (请你画出图形并直接写出结果,图没画或画错均不得分).
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
探究:(1)如图甲,已知△ABC中∠C=90°,你能把△ABC分割成2个与它自己相似的小直角三角形吗?若能,请在图甲中画出分割线,并说明理由.
(2)一般地,“任意三角形都是自相似图形”,只要顺次连结三角形各边中点,则可将原三分割为四个都与它自己相似的小三角形.我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割,称为1阶分割(如图1);把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割,称为2阶分割(如图2)……依次规则操作下去.n阶分割后得到的每一个小三角形都是全等三角形(n为正整数),设此时小三角形的面积为Sn.
①若△DEF的面积为1000,当n为何值时,3<Sn<4?
(请用计算器进行探索,要求至少写出二次的尝试估算过程)
②当n>1时,请写出一个反映Sn-1,Sn,Sn+1之间关系的等式(不必证明)

数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答:
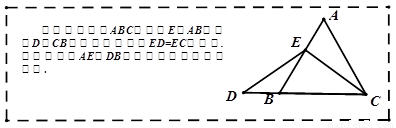
1.特殊情况,探索结论.
当点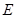 为
为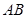 的中点时,确定线段
的中点时,确定线段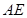 与
与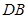 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论: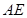
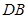 (填“>”,“<”或“=”).
(填“>”,“<”或“=”).
2.特例启发,解答题目[来源:学_科_网]
解:题目中,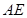 与
与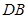 的大小关系是:
的大小关系是: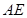
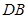 (填“>”,“<”或“=”).理由如下:
(填“>”,“<”或“=”).理由如下:
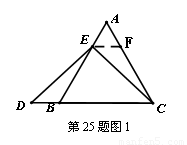
如图1,过点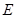 作
作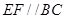 ,交
,交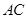 于点
于点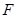 .(请你完成以下解答过程)
.(请你完成以下解答过程)
3.拓展结论,设计新题[来源:ZXXK]
在等边三角形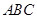 中,点
中,点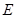 在直线
在直线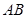 上,点
上,点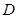 在直线
在直线 上,且
上,且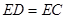 .若
.若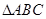 的边长为1,
的边长为1,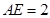 ,则
,则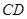 的长为
(请你画出图形并直接写出结果,图没画或画错均不得分).
的长为
(请你画出图形并直接写出结果,图没画或画错均不得分).
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
探究:(1)如图甲,已知△ABC中∠C=90°,你能把△ABC分割成2个与它自己相似的小直角三角形吗?若能,请在图甲中画出分割线,并说明理由.
(2)一般地,“任意三角形都是自相似图形”,只要顺次连结三角形各边中点,则可将原三分割为四个都与它自己相似的小三角形.我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割,称为1阶分割(如图1);把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割,称为2阶分割(如图2)……依次规则操作下去.n阶分割后得到的每一个小三角形都是全等三角形(n为正整数),设此时小三角形的面积为Sn.
①若△DEF的面积为1000,当n为何值时,3<Sn<4?
(请用计算器进行探索,要求至少写出二次的尝试估算过程)
②当n>1时,请写出一个反映Sn-1,Sn,Sn+1之间关系的等式(不必证明)


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com