
题目列表(包括答案和解析)

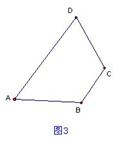
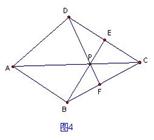
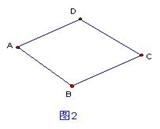
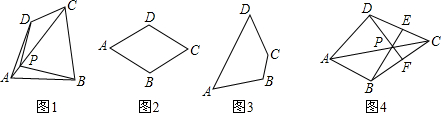
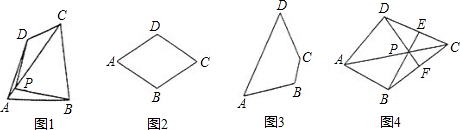
边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图l,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点. (1)如图2,画出菱形ABCD的一个准等距点. (2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法). (3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形AB CD的准等距点. (4)试研究四边形的准等距点个数的情况(说出相应四边形的特征及准等距点的个数,不必证明).


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com