题目列表(包括答案和解析)
探索研究
(1
）观察一列数2，4，8，16，32，…，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是 ；根据此规律，如果
（
为正整数）表示这个数列的第
项，那么
，
；
(2
）如果欲求
的值，可令
将①式两边同乘以3，得
………………………………………………………②
由②减去①式，得
(3
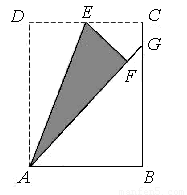
）用由特殊到一般的方法知：若数列
，从第二项开始每一项与前一项之比的常数为
，则
(用含
的代数式表示），如果这个常数
，那么
(用含的代数式表示）．
如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE，且点F在矩形ABCD内部．将AF延长交边BC于点G．若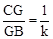
，则
（用含k的代数式表示）．
学校 幼儿园 小学 中学 特殊教育 高等学校
百分比 35% 32% 24% 4% 5%
若高等学校有40所，则该市共有学校________所，中学有________所，用扇形统计图表示时，幼儿园和高等学校所对的圆心角分别是________度和________度.
实践与探索课上，老师布置了这样一道题：
有100米长的篱笆材料，想围成一矩形露天仓库，要求面积不小于600平方米，在场地的北面有一堵长50米的旧墙．有人用这个篱笆围一个长40米，宽10米的矩形仓库，但面积只有400平方米，不合要求．现在请你设计矩形仓库的长和宽，使它符合要求．
经过同学们一天的实践与思考，老师收到了如下几种设计方案：
(1)如果设矩形的宽为x米，则用于长的篱笆为
＝(50－x)米，这时面积S＝x(50－x)．
当S＝600时，由x(50－x)＝600，得x2－50x＋600＝0，解得x1＝20，x2＝30．
检验后知x＝20符合要求．
(2)根据在周长相等的条件下，正方形面积大于矩形面积，所以设计成正方形仓库，它的边长为x米，则4x＝100，x＝25．这时面积达到625米，当然符合要求．
(3)如果利用场地北面的那堵旧墙，取矩形的长与旧墙平行，设与墙垂直的矩形一边长为x米，则另一边为100－2x，如图．
因为旧墙长50米，所以100－2x≤50．即x≥25米．若S＝600平方米，则由x(100－2x)＝600，即x2－50x＋300＝0，解得x1＝25＋
，x2＝25－．根据x≥25，舍去x2＝25－．
所以，利用旧墙，取矩形垂直于旧墙一边长为25＋米(约43米)，另一边长约14米，符合要求．
(4)如果充分利用北面旧墙，即矩形一边是50米旧墙时，用100米篱笆围成矩形仓库，则矩形另一边长为25米，这时矩形面积为S＝50×25＝1250(平方米)．即面积可达1250平方米，符合设计要求．
还可以有其他一些符合要求的设计方案．请你试试看．
如图1，△ABC为等边三角形，面积为S．D1、E1、F1分别是△ABC三边上的点，且
，连结
、
、
，可得△
是等边三角形，此时△
的面积
，△的面积
．
⑴ 当D2、E2、F2分别是等边△ABC三边上的点，且
时如图2，
① 求证：△
是等边三角形；
② 若用S表示△
的面积
，则S2
= ；
若用S表示△
的面积
，则= ．
⑵ 按照上述思路探索下去，并填空：
当Dn、En、Fn分别是等边△ABC三边上的的点，
时，（n为正整数）
△DnEnFn
是 三角形；若用S表示△ADnFn的面积Sn，则Sn = ；
若用S表示△DnEnFn的面积
，则
= ．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com