香港的“公屋制度”,解决了30%以上,约200万人口的居住问题.内地对公租房建设也多有讨论,但尚未有一个城市真正的大规模尝试.重庆建设公共租赁住房,意在重点解决“夹心层”住房问题,力争城市保障性住房的“全覆盖”.经过认真调研,重庆市政府决定,计划10年内解决低收入人群的住房问题.在内地城市中首开了实施“公租房”制度,根据政府安排,前6年年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是
y=-x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是
y=x+5,(x单位:年,7≤x≤10且x为整数);由于部分已修公租房设施老化需要维修更新,经测算,需要投入更新设备的资金p(单位:百万元)与年分x的数量关系满足p=30x-34,假设每年的公租房全部出租完,另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/㎡)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
| z(元/㎡) |
50 |
52 |
54 |
56 |
58 |
… |
| x(年) |
1 |
2 |
3 |
4 |
5 |
… |
(1)求出z与x的函数关系式;
(2)求政府在第几年投入的公租房所获利润最多,最多为多少百万元?
(3)若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第8年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高a%,这样可解决住房的人数将比第6年增加1.35a%,求a的值(结果保留整数)
(参考数据:
=61.87,
=61.88,
=61.89)

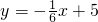 ;7≤x≤10时,
;7≤x≤10时,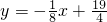 .同时,政府每年将向租户收取一定的租金,假设每年的公租房全部出租完,另外随着物价上涨等因素的影响,每年的租金也会随之上调,预测:第x年竣工并投入使用的公租房租金z(元/m2)与时间x(年)满足以下表:
.同时,政府每年将向租户收取一定的租金,假设每年的公租房全部出租完,另外随着物价上涨等因素的影响,每年的租金也会随之上调,预测:第x年竣工并投入使用的公租房租金z(元/m2)与时间x(年)满足以下表: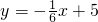 ,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是
,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是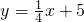 ,(x单位:年,7≤x≤10且x为整数);由于部分已修公租房设施老化需要维修更新,经测算,需要投入更新设备的资金p(单位:百万元)与年分x的数量关系满足p=30x-34,假设每年的公租房全部出租完,另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/㎡)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
,(x单位:年,7≤x≤10且x为整数);由于部分已修公租房设施老化需要维修更新,经测算,需要投入更新设备的资金p(单位:百万元)与年分x的数量关系满足p=30x-34,假设每年的公租房全部出租完,另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/㎡)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表: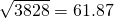 ,
,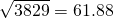 ,
,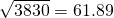 )
)