
题目列表(包括答案和解析)
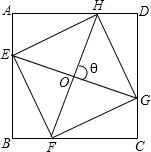 ∠CFH都是锐角,已知EG=k,FH=l,四边形EFGH的面积为S,
∠CFH都是锐角,已知EG=k,FH=l,四边形EFGH的面积为S,| 2S | kl |
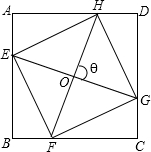 ∠CFH都是锐角,已知EG=k,FH=l,四边形EFGH的面积为S,
∠CFH都是锐角,已知EG=k,FH=l,四边形EFGH的面积为S,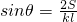 ;
; ∠CFH都是锐角,已知EG=k,FH=l,四边形EFGH的面积为S,
∠CFH都是锐角,已知EG=k,FH=l,四边形EFGH的面积为S,| 2S |
| kl |
|
|

 我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.
我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.


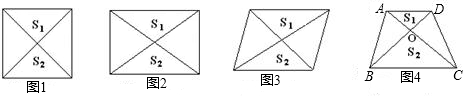
| S |
| S1 |
| S2 |
| S |
| S1 |
| S2 |
| S |
| S1 |
| S2 |
| S |
| S1 |
| S2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com