
题目列表(包括答案和解析)
 如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2-CF2取最大值时,求tan∠DCF的值.
分析 (1)利用60°角![]() 的正弦值列式计算即可得解;
的正弦值列式计算即可得解;
(2)①连接CF并延长交BA的延长线于点G,利用“角边角”证明△AFG和△CFD全等,根据全等三角形对应边相等可得CF=GF,AG=CD,再利用直角三角形斜边上的中线等于斜边的一半可得EF=GF,再根据A![]() B、BC的长度可得AG=AF,然后利用等边对等角的性质可得∠AEF=∠G=∠AFG,
B、BC的长度可得AG=AF,然后利用等边对等角的性质可得∠AEF=∠G=∠AFG,![]() 根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EFC=2∠G,然后推出∠EFD=3∠AEF,从而得解;
根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EFC=2∠G,然后推出∠EFD=3∠AEF,从而得解;
②设BE=x,在Rt△BCE中,利用勾股定理表示出CE2,表示出EG的长度,在Rt△CEG中,利用勾股定理表示出CG2,从而得到CF2,然后相减并整理,再根据二次函数的最值问题解答.
求证:(1)△BDE是等边三角形;
(2)若∠BDC=120°,猜想四边形BDCE是怎样的四边形,并证明你的猜想.
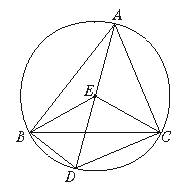
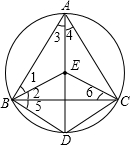 ,CE且∠BDA=60°.
,CE且∠BDA=60°.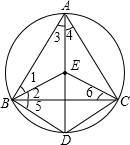 ,CE且∠BDA=60°.
,CE且∠BDA=60°.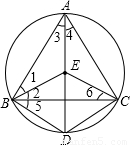
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com