如图的格点图中，每行（列）相邻两个格点之间都相距1个长度单位．
（1）如图，格点C与格点A、B构成的三角形ABC的面积是2，还有一些格点与格点A、B构成的三角形面积也是2，请找出所有这样的格点，并在图上标示出来．

（2）有些格点与格点A、B可以构成等腰三角形ABD，请你找出所有这样的格点D，并在图中标出．

（3）问题（2）所得到的等腰三角形中有没有等边三角形？如有，将它们标示出来；
如没有，思考：在下面的8*8格点图中，是否存在以格点为顶点的等边三角形，如果存在，请标示出来，如果不存在，说明理由，一般地，对于任意大的格点图（如100*100个点的格点图），这个结论是否成立？

（4）问题（2）所得到的等腰三角形中有没有以AB为腰的等腰直角三角形，有没有以AB为底的等腰直角三角形？
一般地，在充分大的格点图中，对于任意给定的两个格点，是否一定存在以这两个格点所在线段为腰的等腰直角三角形？如果一定有，说明你的构造方法；如果不一定有，思考：对于什么样的两点（即两点的坐标之间满足什么条件时）有．
在充分大的格点图中，对于任意给定的两个格点，是否一定存在以这两个格点所在线段为底的等腰直角三角形？如果一定有，说明你的构造方法；如果不一定有，思考：对于什么样的两点（即两点的坐标之间满足什么条件时）有．

如图（1），△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=AC=EF=3，∠BAC=∠DEF=90º，固定△ABC，将△DEF绕点A顺时针旋转，当DF边与AB边重合时，旋转中止．现不考虑旋转开始和结束时重合的情况，设DE，DF(或它们的延长线)分别交BC(或它的延长线) 于G，H点，如图(2)

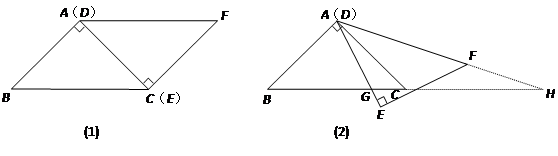
（1）问：始终与△AGC相似的三角形有            及           ；

（2）设CG=x，BH=y，求y关于x的函数关系式（只要求根据图(2)的情形说明理由）；

（3）问：当x为何值时，△AGH是等腰三角形。

【解析】（1）根据△ABC与△EFD为等腰直角三角形，AC与DE重合，利用相似三角形的判定定理即可得出结论．

（2）由△AGC∽△HAB，利用其对应边成比例列出关于x、y的关系式：3：y=x：3即可．

（3）此题要采用分类讨论的思想，当CG＜1/2BC时，当CG=1/2BC时，当CG＞1/2BC时分别得出即可

如图（1），△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=AC=EF=3，∠BAC=∠DEF=90º，固定△ABC，将△DEF绕点A顺时针旋转，当DF边与AB边重合时，旋转中止．现不考虑旋转开始和结束时重合的情况，设DE，DF(或它们的延长线)分别交BC(或它的延长线) 于G，H点，如图(2)

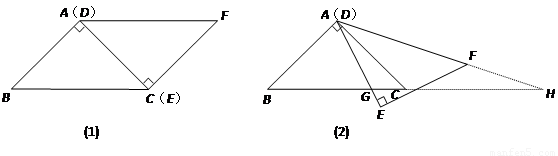
（1）问：始终与△AGC相似的三角形有             及            ；

（2）设CG=x，BH=y，求y关于x的函数关系式（只要求根据图(2)的情形说明理由）；

（3）问：当x为何值时，△AGH是等腰三角形。

【解析】（1）根据△ABC与△EFD为等腰直角三角形，AC与DE重合，利用相似三角形的判定定理即可得出结论．

（2）由△AGC∽△HAB，利用其对应边成比例列出关于x、y的关系式：3：y=x：3即可．

（3）此题要采用分类讨论的思想，当CG＜1/2BC时，当CG=1/2BC时，当CG＞1/2BC时分别得出即可