
题目列表(包括答案和解析)
观察下列各式:(x-1)(x+1)=x –1
–1
(x-1)(x +x+1)=x
+x+1)=x -1
-1
(x-1)(x +x
+x +x+1)=x
+x+1)=x -1
-1
(x-1)(x +x
+x +x
+x +x+1)=x
+x+1)=x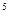 -1
-1
(1) 根据前面各式的规律可得:(x-1)(x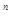 +x
+x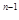 +…+x+1)= 、(其中n为正整数)
+…+x+1)= 、(其中n为正整数)
(2)根据(1)求:1+2+2 +2
+2 +…+2
+…+2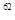 +2
+2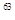 的值,并求出它的个位数字。
的值,并求出它的个位数字。
观察下列各式:
(x﹣1)(x+1)=x2﹣1,
(x﹣1)(x2+x+1)=x3﹣1,
(x﹣1)(x3+x2+x+1)=x4﹣1,
(x﹣1)(x4+x3+x2+x+1)=x5﹣1,
(1)根据前面各式的规律可得:(x﹣1)(xn+xn﹣1+…+x2+x+1)= _________ (其中n为正整数).
(2)根据(1)求1+2+22+23+…+262+263的值,并求出它的个位数字.
观察下列各式:
(x﹣1)(x+1)=x2﹣1,
(x﹣1)(x2+x+1)=x3﹣1,
(x﹣1)(x3+x2+x+1)=x4﹣1,
(x﹣1)(x4+x3+x2+x+1)=x5﹣1,
(1)根据前面各式的规律可得:(x﹣1)(xn+xn﹣1+…+x2+x+1)= _________ (其中n为正整数).
(2)根据(1)求1+2+22+23+…+262+263的值,并求出它的个位数字.
观察下列各式: (x-1)(x+1)=x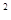 –1
–1
(x-1)(x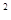 +x+1)=x
+x+1)=x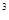 -1
-1
(x-1)(x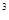 +x
+x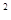 +x+1)=x
+x+1)=x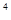 -1
-1
(x-1)(x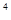 +x
+x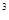 +x
+x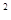 +x+1)=x
+x+1)=x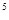 -1
-1
(1) 根据前面各式的规律可得:(x-1)(x +x
+x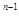 +…+x+1)= 、(其中n为正整数)
+…+x+1)= 、(其中n为正整数)
(2)根据(1)求:1+2+2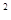 +2
+2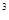 +…+2
+…+2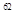 +2
+2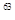 的值,并求出它的个位数字。
的值,并求出它的个位数字。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com