练习册

  • 练习册
  • 试题
    23．如图.要测量池塘两端A,B间的距离,可以在陆地上取一点可以直接到达A和B的点C.连接AC并延长到D.使CD=CA.连接BC并延长到E.使CE=CB,连接DE.那么量出DE的长就是A.B的距离.请在下图基础上完成作图并说明理由. 24. 如图.AD是△ABC的角平分线,DE⊥AB.DF⊥AC.垂足分别为E.F.连接E,F,求证明:AD平分∠EDF, (3)请你猜想.AD与EF有何关系.并说明理由. 【查看更多】

     

    题目列表(包括答案和解析)

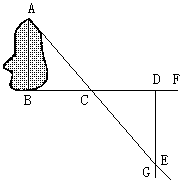
    如图，要测量一个池塘两端A、B之间的距离，可以在AB的垂线BF上取两点C、D，使CD=BC，再过D点作出BF的垂线DG，并在DG上找一点E，使A、C、E在一条直线上，这时测得的DE长就是A、B间的距离．你能说出这是为什么吗?

    查看答案和解析>>

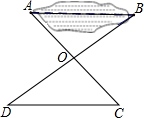    如图，为了测量池塘两端A，B的距离，小红在地面上选择了点O，C，D，使OA=OC，OB=OD，且点A，O，C和点B，O，D分别都在一条直线上，只要量出CD的长，就可以知道A，B之间的距离．那么判定△AOB≌△COD的理由是
    SAS
    SAS
    ．

    查看答案和解析>>

    如图，有一个池塘，要测量池塘两端A，B的距离，可先在平地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD＝CA．连接BC并延长到E，使EC＝CB，连接DE，量出DE的长，就是A，B间的距离．写出你的证明．

    查看答案和解析>>

    为了测量一池塘的两端A，B之间的距离，同学们想出了如下的两种方案：

    ①如图1，先在平地上取一个可直接到达A，B的点C，再连接AC，BC，并分别延长AC至点D，BC至点E，使DC=AC，EC=BC，最后量出DE的距离就是AB的长；
    ②如图2，过点B作AB的垂线BF，在BF上取C，D两点，使BC=CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即是AB的距离．
    问：
    （1）方案①是否可行？
    可行
    可行
    ，理由是
    SAS可证明△ACB≌△DCE，再根据全等三角形的性质可得AB=ED
    SAS可证明△ACB≌△DCE，再根据全等三角形的性质可得AB=ED
    ；
    （2）方案②是否可行？
    可行
    可行
    ，理由是
    ASA可证明△ACB≌△DCE，再根据全等三角形的性质可得AB=ED
    ASA可证明△ACB≌△DCE，再根据全等三角形的性质可得AB=ED
    ；
    （3）小明说在方案②中，并不一定需要BF⊥AB，DE⊥BF，只需要
    AB∥DE
    AB∥DE
    就可以了，请把小明所说的条件补上．

    查看答案和解析>>

    如图所示，有一个池塘，若要测池塘两端A、B间的距离，可先在平地上取一个可以直接到达A和B的点C，连结AC并延长到D，使CD＝CA．连结BC并延长到E，使CE＝CB．连结DE，量出DE的长，这个长就是A、B之间的距离．

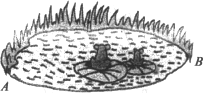
    (1)按题中的要求画图．

    (2)说明DE＝AB的理由，并试着把说明的过程写出来．

    查看答案和解析>>


    同步练习册答案