（本小题满分8分）

　已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE = AF．

（1）求证：BE = DF；

（2）连接AC交EF于点O，延长OC至点M，使OM = OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．

（本小题满分8分）
　已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE = AF．

（1）求证：BE = DF；
（2）连接AC交EF于点O，延长OC至点M，使OM = OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．

（本小题满分8分）

　已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE = AF．

（1）求证：BE = DF；

（2）连接AC交EF于点O，延长OC至点M，使OM = OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．

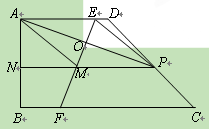
（11·珠海）（本题满分9分）如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，

AD＝AB＝1，BC＝2．将点A折叠到CD边上，记折叠后A点对应的点为P（P与D点不重

合），折痕EF只与边AD、BC相交，交点分别为E、F．过点P作PN∥BC交AB于N、交

EF于M，连结PA、PE、AM，EF与PA相交于O．

（1）指出四边形PEAM的形状（不需证明）；

（2）记∠EPM＝a，△AOM、△AMN的面积分别为S₁、S₂．