1、如图所示，在△ABD和△ACE中，有下列四个论断：①AB=AC，②AD=AE  ③∠B=∠C，④BD=CE．
请以其中三个论断作为条件，余下一下作为结论，写出一个正确的数学题（用序号表示）并证明．

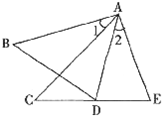32、如图，在△ABD和△ACE中，有下列四个论断：①AB=AC；②AD=AE；③∠1=∠2；④BD=CE．请你以其中三个作为条件，余下的一个作为结论，编一道数学题，并写出解答过程．（要求写出已知，求证及证明过程）

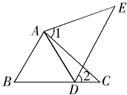48、如图，已知：∠1=∠2，要证明△ABC≌△ADE，还需补充的条件是（　　）

23、如图，给出四个等式：①AE=AD；②AB=AC；③OB=OC：④∠B=∠C．现请你选取其中的三个，以某两个作为已知条件，另一个作为结论．
（1）试写出一个正确的命题，并加以证明；
（2）请你写出三个正确命题．

21、如图，给出四个等式：①AE=AD；②AB=AC；③OB=OC；④∠B=∠C． 现选取其中的三个，以两个作为已知条件，另一个作为结论组成命题．
（1）请你写出两个真命题（用序号填空）．
真命题1：已知求证：．
真命题2：已知求证：．
（2）请你选择其中的一个真命题加以证明；
我选择真命题．
证明：