
题目列表(包括答案和解析)
如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是![]() cm2和
cm2和![]() cm2,则Rt△ABC的面积为( )cm2.
cm2,则Rt△ABC的面积为( )cm2.
A.24 B.30 C.48 D.60
 |
如图
1,在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°.若BC=1,则根据“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”以及勾股定理容易得到AB=________,AC=________.因此,含30°角的直角三角形三边(从小到大)之比为________;同样,如图2,含45°角的直角三角形三边(从小到大)之比为________.这样结合三角函数的定义可以推导得到30°、45°、60°角的三角函数值.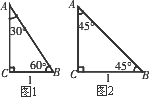
如图
1,在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°.若BC=1,则根据在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半及勾股定理容易得到AB=________,AC=________.因此,含30°角的直角三角形三边(从小到大)之比为________;同样,如图2,含45°角的直角三角形三边(从小到大)之比为________.这样结合三角函数的定义可以推导得到30°、45°、60°角的三角函数值.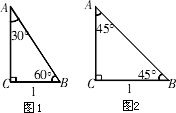
问题背景:
如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是射线CB上任意一点,△ADE是等边三角形,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系.
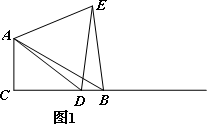
探究结论:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
(1)当点D与点C重合时(如图2),请你补全图形.由∠BAC的度数为________,点E落在AB上,容易得出BE与DE之间的数量关系为________;
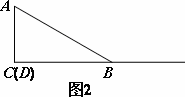
(2)当点D在如图3的位置时,请你画出图形,研究线段BE与DE之间的数量关系是否与(1)中的结论相同,写出你的猜想并加以证明.
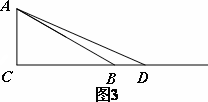
拓展应用:
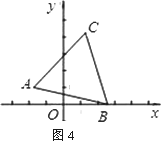
(3)如图4,在平面直角坐标系xOy中,点A的坐标为(![]() ,1),点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x的函数关系式.
,1),点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x的函数关系式.
如图①所示,将一个正三角形纸片沿着它的一条边上的高剪开,得到如图②所示的两个全等的Rt△ABC、Rt△DEF.

(1)根据正三角形的性质可知:在图②中,∠ABC=∠DEF=30°,AB=DE=2AC=2DF.由此请你归纳一下在含30°角的直角三角形中,30°角所对的直角边与斜边之间的关系:
在含30°角的直角三角形中,30°角所对的直角边________;
(2)将这两个直角三角形纸片按如图③放置,使点B、D重合,点F在BC上.固定纸片DEF,将△ABC绕点F逆时针旋转角α(0°<α<90°),使四边形ACDE为以ED为底的梯形(如图④所示),求此时α的值;
(3)猜想图④中AE与CD之间的大小关系,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com